Question

Given,4 point-size spheres each of mass 1 kg are placed on a turntable and are connected by 4 strings, each of length a to form a square. If the spheres are rotated with an angular velocity of $\dfrac{1}{2\pi }\,{rev}/{sec}\;$, the tension in the connecting strings in newton is:
$\begin{aligned} & A.\,\,\,a \\\ & B.\,\,\,\dfrac{a}{2} \\\ & C.\,\,\,\dfrac{a}{\sqrt{2}} \\\ & D.\,\,\,\sqrt{2a} \\\ \end{aligned}$

Answer 1

To get the solution for this question, first get the centrifugal force that is applied on the sphere due to the two strings attached to it and once the centrifugal force is calculated then using the resultant tension, the value of tension on the string can be received. The formula for centrifugal force is known and the value of the variable is also mentioned in the question, which will help to get the value of the force.
Formula used:
$F=mr{{\omega }^{2}}$

Complete answer:
4 point-size steel spheres each of mass 1 kg are placed on a turntable and are connected by 4 strings, each of length a to form a square, such that every sphere is connected to two strings that are right angled to each other.

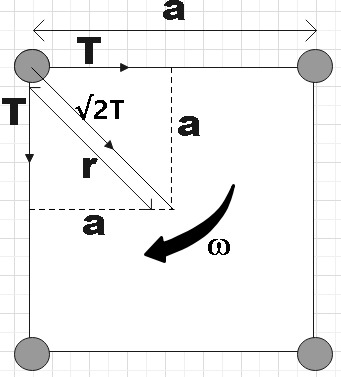
The resultant tension of the string gives the centrifugal force to a sphere, such that
${{T}_{res}}={{F}_{{{c}_{{}}}}}$
The resultant tension due to tension T in the adjacent strings will be,
${{T}_{res}}=\sqrt{{{T}^{2}}+{{T}^{2}}+2{{T}^{2}}\cos 90}$
$\therefore {{T}_{res}}=\sqrt{2}T$ ……………………………………………. (1)
Now, Centrifugal force is given by,
${{F}_{c}}=mr{{\omega }^{2}}$
where, ‘m’ is the mass of the sphere which is given 1kg according to the question.
‘r’ is the radius of the circle, which can also be written as the distance between the mass and center of the square.
‘$\omega$’ is angular velocity.
According to the question,
$\omega =\dfrac{1}{2\pi }\,{rev}/{sec}\;=\dfrac{1}{2\pi }\,{\times \,2\pi \,rad}/{sec}\;={1\,rad}/{sec}\;$
And radius of the circle is equal to the half of the diagonal of a square, which is
$\begin{aligned} & \text{Radius of Circle = }\dfrac{1}{2}\times (\text{Diagonal of Square}) \\\ & \Rightarrow \text{Radius of Circle = }\dfrac{1}{2}\times (\sqrt{{{a}^{2}}+{{a}^{2}}}) \\\ & \Rightarrow \text{Radius of Circle = }\dfrac{1}{2}\times (\sqrt{2{{a}^{2}}}) \\\ & \Rightarrow \text{Radius of Circle = }\dfrac{1}{2}\times (\sqrt{2}a) \\\ & \therefore \text{Radius of Circle = }\dfrac{a}{\sqrt{2}} \\\ \end{aligned}$
Since, we know the mass, radius, and angular velocity, so the centrifugal force can be found by substituting the value in the force equation, which is shown below:
$\begin{aligned} & {{F}_{c}}=(1\times \dfrac{a}{\sqrt{2}}\times {{1}^{2}})\,N \\\ & \therefore {{F}_{c}}=\dfrac{a}{\sqrt{2}}\,N \\\ \end{aligned}$………………………………………….. (2)
Hence, the tension in the connected strings can be obtained by equating equations (1) and (2). So,
$\sqrt{2}T=\dfrac{a}{\sqrt{2}}$
$T=\dfrac{a}{2}$

Therefore, the correct answer is Option (B).

Note:
This type of question is frequently asked in exams, where in place of giving the diagram all the details are explained in the question. After reading the question properly, it becomes easy to imagine the diagram of this question, which will help to get the answer easily. But if the question is not understood properly, then imagining the diagram becomes difficult due to which reaching the answer becomes difficult.