Solveeit Logo
Login

Question

Question: Given, 1.1 \(c{{m}^{3}}\) of gold is drawn into a wire of 0.1 mm in diameter. Find the length of the...

Given, 1.1 cm3c{{m}^{3}} of gold is drawn into a wire of 0.1 mm in diameter. Find the length of the wire in meters.

Explanation

Solution

Hint: We know that wire is in the form of a cylinder. The diameter of the cylinder is given as 0.1 mm. Also, the volume of the cylinder is given. We can assume the length of the wire to be L. Using the formula for the volume of a cylinder which is Vol=πr2LVol=\pi {{r}^{2}}L, we can find the value of L.

Complete step by step answer:

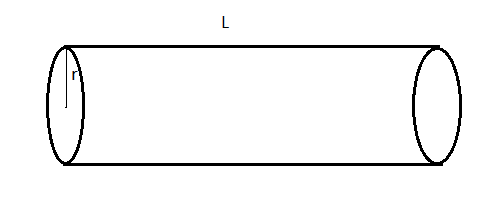
Since, we have the formula for the volume of a cylinder as:
Vol=πr2L.................(1)Vol=\pi {{r}^{2}}L.................\left( 1 \right)
Here, we have the value of the diameter of the cylinder which is = 0.1 mm.
We know that the radius is half of the diameter. So, r=d2=0.12mm=0.05mmr=\dfrac{d}{2}=\dfrac{0.1}{2}mm=0.05mm
Since, the wire is made from the given volume of gold. So, the volume of cylindrical wire will be equal to the given volume of gold.
So, the volume of cylindrical wire is = 1.1 cm31.1\,c{{m}^{3}}
Since, we know that 1cm = 10 mm
So, 1 cm3=(10mm)3             =1000 mm3 \begin{aligned} & 1\,c{{m}^{3}}={{\left( 10mm \right)}^{3}} \\\ & \,\,\,\,\,\,\,\,\,\,\,\,=1000\,m{{m}^{3}} \\\ \end{aligned}
Therefore, 1.1 cm3=1.1×1000 mm3                 =1100 mm3 \begin{aligned} & 1.1\,c{{m}^{3}}=1.1\times 1000\,m{{m}^{3}} \\\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=1100\,m{{m}^{3}} \\\ \end{aligned}
On substituting the values of volume and the radius of the cylinder in equation (1), we get:
1100=π×0.05×L ⇒1100=227×0.0025×L ⇒L=1100×722×0.0025            =1,40,000 \begin{aligned} & 1100=\pi \times 0.05\times L \\\ & \Rightarrow 1100=\dfrac{22}{7}\times 0.0025\times L \\\ & \Rightarrow L=\dfrac{1100\times 7}{22\times 0.0025} \\\ & \,\,\,\,\,\,\,\,\,\,\,=1,40,000 \\\ \end{aligned}
So, the length of the wire is =1,40,000 mm.
On dividing this obtained value of length by 1000 to convert the length into meter, we get:
L=1400001000=140 mL=\dfrac{140000}{1000}=140\,m
Hence, the length of this cylindrical wire is 140 m.

Note: Students should note here that the conversion of units is necessary. The unit of the radius of the wire and the volume of the wire must be the same otherwise it can lead to mistakes. Students should remember the correct formula for the volume of a cylinder to avoid unnecessary mistakes.