Question

Give examples of two one-one functions ${{f}_{1}}$ and ${{f}_{2}}$ from R to R such that ${{f}_{1}}+{{f}_{2}}:R\to R$ defined by $\left( {{f}_{1}}+{{f}_{2}} \right)\left( x \right)={{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)$ is not one-one.

Answer 1

Hint: For this question make ${{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=\text{constant}$ as y = k is the easiest function which is not one-one. Take ${{f}_{1}}\left( x \right)$ and ${{f}_{2}}\left( x \right)$ as linear function in x such that ${{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)$ is constant.

Here we have to find two one-one functions ${{f}_{1}}$ and ${{f}_{2}}$ R to R such that $\left( {{f}_{1}}+{{f}_{2}} \right)x={{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)$ is not one-one.
We know that one-one function is a function that maps distinct elements of its domain to distinct elements of its co-domain that is for a particular value of x, there is a particular value of y and that value of y should not repeat for any other value of x.
Now, we have to make ${{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)$ such that it is not one-one.
We know that $f\left( x \right)=\text{constant}$ is the easiest function which is not one-one because its value of y keeps getting repeated for all values of x.

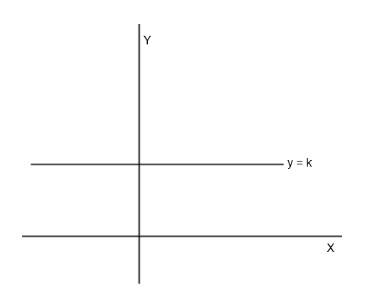
Therefore, we will choose ${{f}_{1}}\left( x \right)$ and ${{f}_{2}}\left( x \right)$ such that
${{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=k$
Now, we are given that ${{f}_{1}}\left( x \right)$ and ${{f}_{2}}\left( x \right)$ must be one-one.
We know that the easiest one-one function is $y=ax+b:R\to R$ where a and b are constants as it gives different values of y for different values of x.
Therefore, we take ${{f}_{1}}\left( x \right)=9x+5$.
Now to make ${{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)$ constant, 9x must disappear.
Therefore, we take ${{f}_{2}}\left( x \right)=-9x+8$.

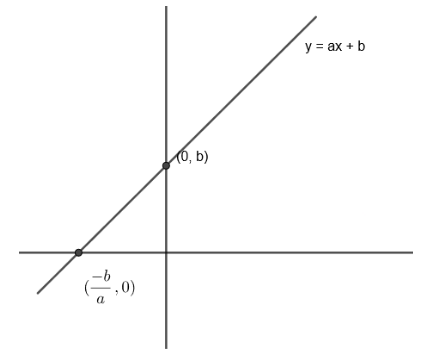
Therefore, we get ${{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=\left( 9x+5 \right)+\left( -9x+8 \right)$.
$\Rightarrow {{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=13$
Therefore, finally we get
${{f}_{1}}\left( x \right)=9x+5$
${{f}_{2}}\left( x \right)=-9x+8$
which are one-one functions.
Also, we get ${{f}_{1}}\left( x \right)+{{f}_{2}}\left( x \right)=13$ which is not a one-one function.

Note: Students could also check if a function is one-one or not by making the line on the graph of the function which is parallel to the x axis. If this line cuts the graph just 1 time then, it is one-one function, otherwise it is not one-one.