Question
Question: Give a few electric flux examples with explanations....
Give a few electric flux examples with explanations.
Solution
Electric flux means the number of electric field lines passing through a specific surface area. The direction of the surface is always perpendicular to its area. We know electric field lines emerge from positive charge and terminate to negative charge. Also, the field lines entering the closed surface imparts negative flux and field lines exiting the closed surface imparts positive flux.
Formula used:
ϕE=E⋅S=EScosθ
Here, ϕE is flux of electric field,
E is the magnitude of electric field,
S is the area of the surface and
θ is the angle between electric field lines and the normal to the surface.
Complete step by step solution:
Examples on the electric flux are:
ϕE=E⋅S=EScosθ
Example 1. A plane surface has an area of 5-meter square. If an electric field crosses to the surface and has E= 20 Volt per meter. What will be the electric flux?
Explanation - Using the formula
ϕE=E⋅S=EScosθ
=20×5×cos0o =20×5×1 =100Vm
So, the flux is 100Vm .
Example 2. Consider a planar disc of radius 9cm that makes some angle 300 with the uniform electric field
E=400i(N C−1) . Calculate the flux passing through it.
Explanation - Let the electric field be in the x-axis and normal to the plane be in some direction n which is divided into the x and y directions, as shown in the figure. Using the definition of electric flux, we have:
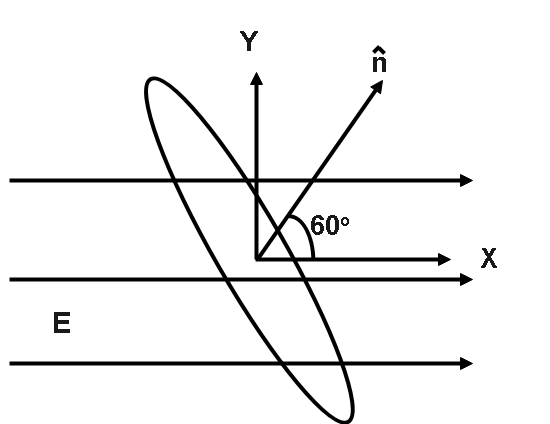
ϕE=∫E⋅nds
Here, ∫ds is total area and since radius is in cm so we convert it into m,
ϕE=400×21×πr2 =200×π×(0.09)2 =5.08938CNm2Note:
Electric flux depends on the surface too. If the surface is curved or plane but the cosine angle it makes is positive, then flux is positive if the angle it makes is greater than 900 then the flux is found to be negative. So, the electric field lines if they enter the closed surface make negative flux while if they exist the closed surface makes positive flux.
