Question
Question: GHJK is a rectangle GH = HI and \[\angle HKJ = {50^0}\]. HLK and GLI are straight lines. Find \[\ang...
GHJK is a rectangle GH = HI and ∠HKJ=500. HLK and GLI are straight lines. Find ∠GLK.
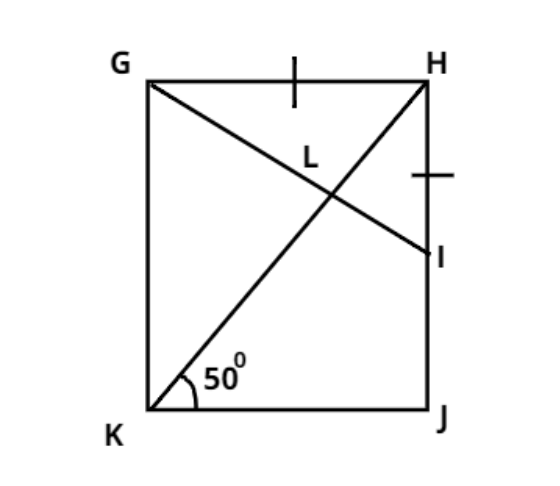
Solution
Hint: In this question it is given that GH = HI and ∠HKJ is also known to us. We need to find ∠GLK.Use the property of the rectangle that the sides of opposite ends are perpendicular to each other at the point of meeting along with the angle sum property of a triangle to get the answer.
Complete step-by-step answer:
As we know in the rectangle all the angles are equal to900.
∴∠GKJ=900=∠GHJ=∠HGK………… (1)
And from figure it is given that ∠HKJ=500
Therefore ∠GKL=∠GKJ−∠HKJ
So substitute the values in above equation we have,
⇒∠GKL=900−500=400…………………….. (2)
Now from figure it is given that GH = HI
Therefore triangle GHI is an isosceles triangle.
Therefore ∠HGI=∠HIG……………… (3)
And we know that in a triangle the sum of all the angles is 180 degrees.
Therefore in triangle GHI
⇒∠GHI+∠HGI+∠HIG=1800
So from equation (1) and (3) we have
⇒900+∠HGI+∠HGI=1800
Now simplify this equation we have,
⇒∠HGI=450
Therefore from figure ∠LGK=∠HGK−∠HGI so substitute the values in above equation we have,
∠LGK=900−450=450……………. (4)
Now in the triangle GLK the sum of all the angles is 180 degrees.
⇒∠GLK+∠LGK+∠GKL=1800
Now from equation (2) and (4) we have.
⇒∠GLK+450+400=1800
⇒∠GLK=1800−850=950
So this is the required value of the angle GLK.
Hence option (C) is correct.
Note: Whenever we face such geometry questions the key concept is simply to have the good understanding of the diagrammatic representation of the geometry given in the problem. This helps finding the specific angles and its relation with other angles with the specific triangles that we are concerned with for that particular problem. This will help getting on the right track to get the answer.
