Question
Question: Consider the circuit shown in the figure. The current I flowing through the 10 $\Omega$ resister is ...
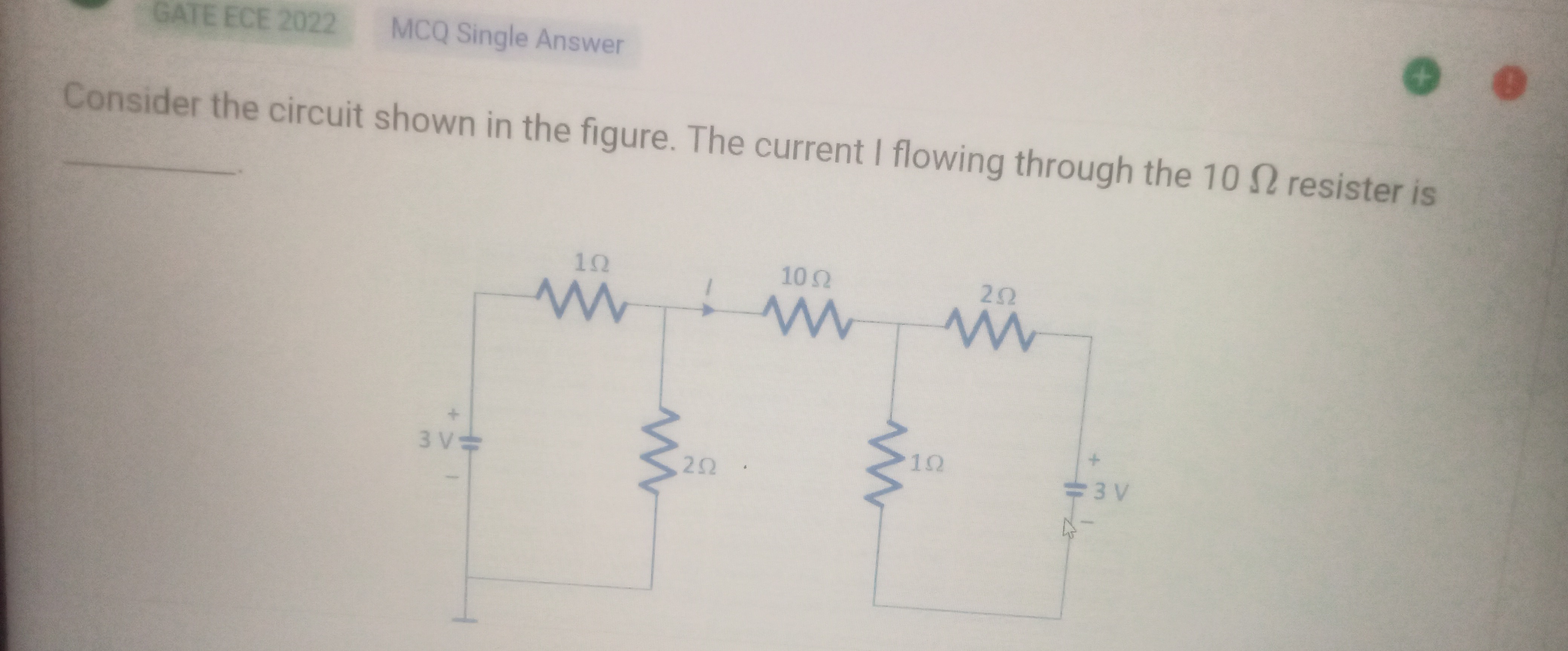
Consider the circuit shown in the figure. The current I flowing through the 10 Ω resister is
3/34 A
Solution
The problem asks us to find the current 'I' flowing through the 10 Ω resistor in the given circuit. We can solve this using nodal analysis.
1. Define Nodes and Ground: Let the bottom line be the ground (0 V). Let the node between the 1 Ω (top left), 2 Ω (bottom left), and 10 Ω resistors be V1. Let the node between the 10 Ω, 2 Ω (top right), and 1 Ω (bottom right) resistors be V2.
2. Apply Kirchhoff's Current Law (KCL) at Node V1: The current leaving node V1 through the 1 Ω resistor (connected to the 3 V source) is 1V1−3. The current leaving node V1 through the 2 Ω resistor (connected to ground) is 2V1−0. The current leaving node V1 through the 10 Ω resistor (connected to V2) is 10V1−V2.
Sum of currents leaving Node V1 equals zero: 1V1−3+2V1+10V1−V2=0 Multiply the entire equation by 10 to clear the denominators: 10(V1−3)+5V1+(V1−V2)=0 10V1−30+5V1+V1−V2=0 16V1−V2=30(Equation 1)
3. Apply Kirchhoff's Current Law (KCL) at Node V2: The current leaving node V2 through the 10 Ω resistor (connected to V1) is 10V2−V1. The current leaving node V2 through the 1 Ω resistor (connected to ground) is 1V2−0. The current leaving node V2 through the 2 Ω resistor (connected to the 3 V source) is 2V2−3.
Sum of currents leaving Node V2 equals zero: 10V2−V1+1V2+2V2−3=0 Multiply the entire equation by 10 to clear the denominators: (V2−V1)+10V2+5(V2−3)=0 V2−V1+10V2+5V2−15=0 −V1+16V2=15(Equation 2)
4. Solve the System of Linear Equations: We have two equations with two unknowns (V1 and V2):
- 16V1−V2=30
- −V1+16V2=15
From Equation 1, express V2 in terms of V1: V2=16V1−30 Substitute this expression for V2 into Equation 2: −V1+16(16V1−30)=15 −V1+256V1−480=15 255V1=495 V1=255495 Simplify the fraction by dividing by 5, then by 3: V1=5199=1733 V Now, substitute the value of V1 back into the expression for V2: V2=16(1733)−30 V2=17528−1730×17 V2=17528−510 V2=1718 V
5. Calculate the Current I: The current I flows through the 10 Ω resistor from V1 to V2. I=10V1−V2 I=101733−1718 I=101733−18 I=101715 I=17×1015 I=17015 Simplify the fraction by dividing by 5: I=343 A
The current I flowing through the 10 Ω resistor is 343 A.
Explanation of the solution: The circuit is analyzed using nodal analysis. Two nodes, V1 and V2, are identified. KCL equations are formulated for each node, expressing the sum of currents leaving the node as zero. This results in a system of two linear equations. These equations are then solved simultaneously to find the node voltages V1 and V2. Finally, the current I through the 10 Ω resistor is calculated using Ohm's law, I=(V1−V2)/10.
Answer: The current I flowing through the 10 Ω resistor is 343 A.
