Question

Game for value of $\frac{Sin 2A + Sin 4A + Sin 6A}{7}$

Answer 1

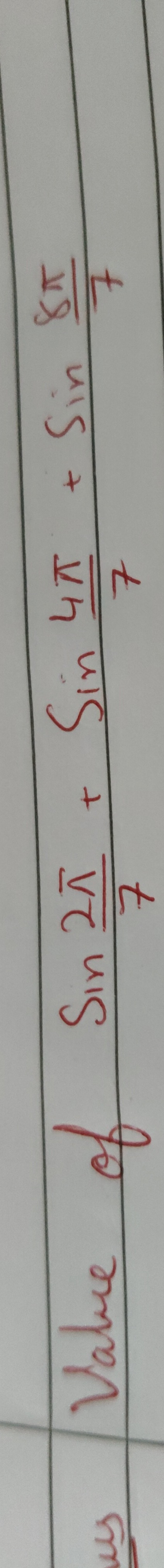
$\frac{\sin 4A (2 \cos 2A + 1)}{7}$

Answer 2

To simplify the given expression $\frac{\sin 2A + \sin 4A + \sin 6A}{7}$, we can use trigonometric sum-to-product identities.

Step 1: Group the terms in the numerator and apply the sum-to-product formula. The sum-to-product formula for $\sin x + \sin y$ is $2 \sin\left(\frac{x+y}{2}\right) \cos\left(\frac{x-y}{2}\right)$. Let's group $\sin 2A$ and $\sin 6A$: $\sin 2A + \sin 6A = 2 \sin\left(\frac{2A+6A}{2}\right) \cos\left(\frac{2A-6A}{2}\right)$ $= 2 \sin\left(\frac{8A}{2}\right) \cos\left(\frac{-4A}{2}\right)$ $= 2 \sin(4A) \cos(-2A)$ Since $\cos(-x) = \cos x$, we have: $\sin 2A + \sin 6A = 2 \sin(4A) \cos(2A)$

Step 2: Substitute this back into the numerator of the original expression. The numerator is $\sin 2A + \sin 4A + \sin 6A$. Substituting the result from Step 1: $\text{Numerator} = 2 \sin(4A) \cos(2A) + \sin 4A$

Step 3: Factor out the common term $\sin 4A$. $\text{Numerator} = \sin 4A (2 \cos 2A + 1)$

Step 4: Write down the complete simplified expression. The given expression is: $\frac{\sin 2A + \sin 4A + \sin 6A}{7} = \frac{\sin 4A (2 \cos 2A + 1)}{7}$

This is the simplified form of the expression. Without any specific value or condition for 'A', the expression cannot be simplified to a numerical constant.

Alternatively, one could recognize the numerator as a sum of sines in an arithmetic progression. The sum of $n$ terms of $\sin(\alpha + (k-1)\beta)$ is given by $S_n = \frac{\sin(n\beta/2)}{\sin(\beta/2)} \sin(\alpha + (n-1)\beta/2)$. Here, $\alpha = 2A$, $\beta = 2A$, and $n=3$. $\text{Numerator} = \frac{\sin(3 \cdot 2A/2)}{\sin(2A/2)} \sin(2A + (3-1)2A/2)$ $= \frac{\sin(3A)}{\sin(A)} \sin(2A + 2A)$ $= \frac{\sin(3A)\sin(4A)}{\sin(A)}$ Thus, the expression is $\frac{\sin(3A)\sin(4A)}{7\sin(A)}$. Both forms are equivalent, as $2\cos(2A)+1 = \frac{\sin(3A)}{\sin(A)}$.

The final answer is $\boxed{\frac{\sin 4A (2 \cos 2A + 1)}{7}}$.

Explanation:

The problem requires simplifying a trigonometric expression. We used the sum-to-product identity $\sin x + \sin y = 2 \sin\left(\frac{x+y}{2}\right) \cos\left(\frac{x-y}{2}\right)$ on the terms $\sin 2A$ and $\sin 6A$. This resulted in $2 \sin 4A \cos 2A$. Adding the remaining term $\sin 4A$ and factoring out $\sin 4A$ led to the simplified numerator $\sin 4A (2 \cos 2A + 1)$. The denominator remains $7$.

Answer:

The value of the expression is $\frac{\sin 4A (2 \cos 2A + 1)}{7}$.