Question
Question: $f(x)=sin^{-1}(sec^{-1}x)$...
f(x)=sin−1(sec−1x)
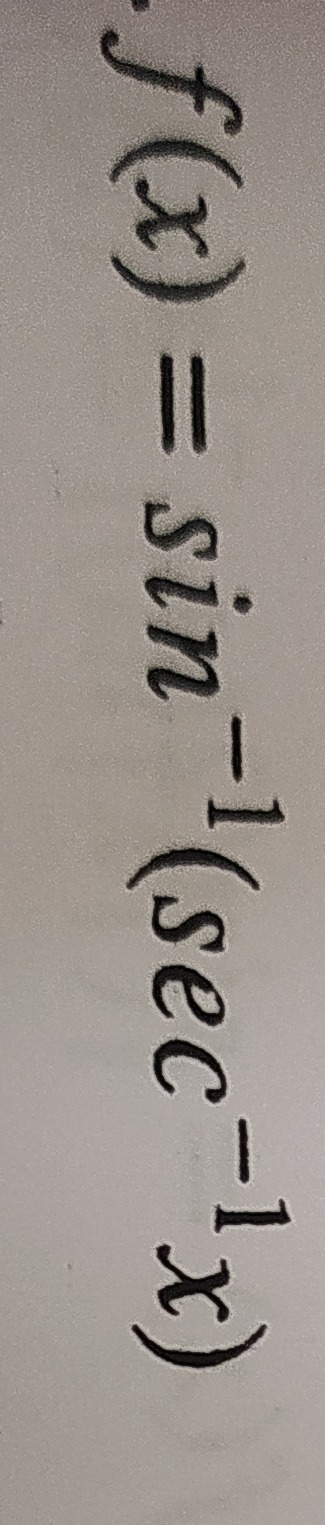
[1, sec(1)]
Solution
The given function is f(x)=sin−1(sec−1x).
For the function f(x) to be defined, two conditions must be satisfied:
- The argument of the outer function, sin−1, must be within its domain. The domain of sin−1(u) is [−1,1]. Thus, we must have sec−1x∈[−1,1].
- The argument of the inner function, sec−1, must be within its domain. The domain of sec−1(x) is (−∞,−1]∪[1,∞). Thus, we must have x∈(−∞,−1]∪[1,∞).
Let's analyze the first condition: sec−1x∈[−1,1]. The principal range of the function sec−1x is [0,π]∖{2π}. We need the values of x such that sec−1x falls within the interval [−1,1]. Let y=sec−1x. We require y∈[−1,1]. Also, from the definition of sec−1x, we know that y must be in the range [0,π]∖{2π}. So, we need y∈[−1,1]∩([0,π]∖{2π}). The intersection of the interval [−1,1] and the set [0,π]∖{2π} is [0,1]. This is because the range [0,π]∖{2π} contains only non-negative values (from 0 up to π≈3.14, excluding π/2≈1.57). The interval [−1,1] contains values from -1 to 1. The common interval is [0,1]. So, the condition sec−1x∈[−1,1] is equivalent to sec−1x∈[0,1]. We need to find the values of x such that 0≤sec−1x≤1.
Let y=sec−1x. We have 0≤y≤1. By the definition of the inverse secant function, x=secy, and y∈[0,π]∖{2π}. The interval [0,1] is a subset of [0,π/2) since 1 radian ≈57.3∘ and π/2 radians ≈90∘. In the interval [0,π/2), the function secy is strictly increasing. Therefore, if we apply the secant function to the inequality 0≤y≤1, the inequality signs are preserved:
sec(0)≤sec(y)≤sec(1)
1≤x≤sec(1)
Now we must consider the second condition for the domain of f(x): x must be in the domain of sec−1x. The domain of sec−1x is (−∞,−1]∪[1,∞).
We need to find the values of x that satisfy both conditions:
- 1≤x≤sec(1)
- x∈(−∞,−1]∪[1,∞)
We need to find the intersection of the interval [1,sec(1)] and the set (−∞,−1]∪[1,∞). Since 1 radian is in the first quadrant (0<1<π/2), cos(1) is positive and 0<cos(1)<1. sec(1)=cos(1)1. Since 0<cos(1)<1, we have sec(1)>1. So, the interval [1,sec(1)] starts at 1 and extends to a value greater than 1. This interval [1,sec(1)] is completely contained within the set [1,∞). The intersection of [1,sec(1)] and (−∞,−1]∪[1,∞) is [1,sec(1)].
Thus, the domain of the function f(x)=sin−1(sec−1x) is [1,sec(1)].
