Question
Question: Determine the domain of the function \[ f(x)=\frac{1}{\sqrt{(x-2)^{2023}\,(x-3)^{2024}\,(x-4)^{2025...
Determine the domain of the function
f(x)=(x−2)2023(x−3)2024(x−4)20251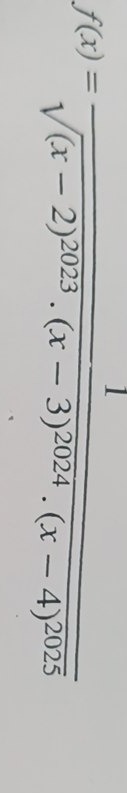
Answer
(−∞,2)∪(4,∞)
Explanation
Solution
Step 1: Identify restrictions
- The expression under the square root must be positive (cannot be zero or negative).
- Exponents:
- (x−2)2023: odd exponent ⇒ sign of (x−2) carries over.
- (x−3)2024: even exponent ⇒ always nonnegative, but zero at x=3 (excluded).
- (x−4)2025: odd exponent ⇒ sign of (x−4) carries over.
Step 2: Exclude zeros of factors
- x=2,3,4 to avoid zero denominator.
Step 3: Positivity condition
We require
since (x−3)2024>0 for all x=3.
Because both exponents are odd, this simplifies to
(x−2)(x−4)>0.Solve (x−2)(x−4)>0:
- Both factors positive ⟹x>4.
- Both factors negative ⟹x<2.
Step 4: Combine intervals
Exclude the points 2,3,4. The domain is
