Question
Question: $f(x)=\begin{cases} x^3 & 2x^2+1 & 1+3x \\ 3x^2+2 & 2x & x^3+6 \\ x^3-x & 4 & x^2-2 \end{cases}$ $2...
f(x)=⎩⎨⎧x33x2+2x3−x2x2+12x41+3xx3+6x2−2
2f(0)+f′(0)=?
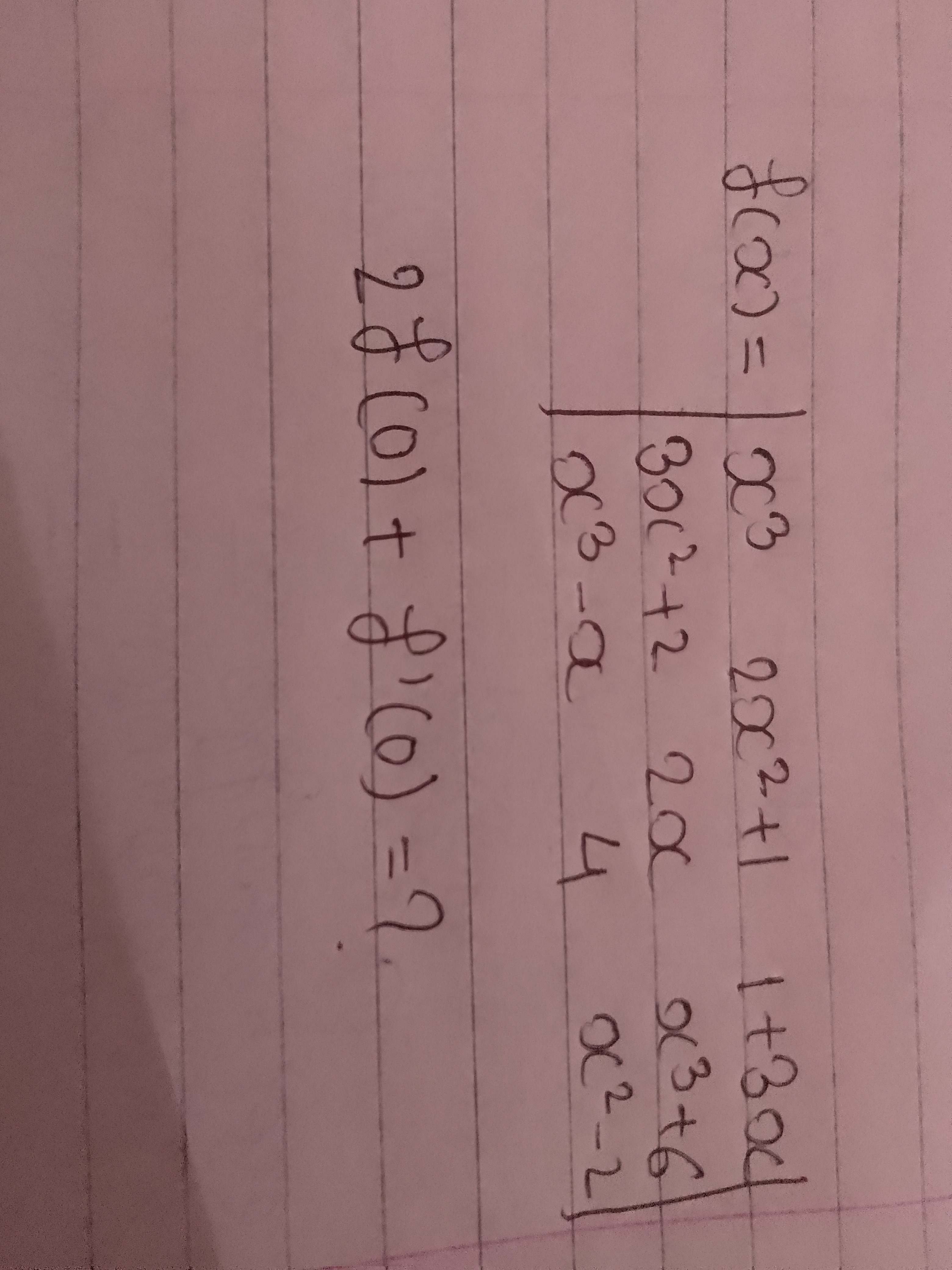
42
Solution
To find the value of 2f(0)+f′(0), we need to first calculate f(0) and f′(0).
The given function is a determinant: f(x)=x33x2+2x3−x2x2+12x41+3xx3+6x2−2
Step 1: Calculate f(0)
Substitute x=0 into the determinant: f(0)=033(0)2+203−02(0)2+12(0)41+3(0)03+602−2=02010416−2
Expanding the determinant along the first column (C1): f(0)=0⋅cofactor(0)−2⋅141−2+0⋅cofactor(0) f(0)=−2⋅((1)(−2)−(1)(4))=−2⋅(−2−4)=−2⋅(−6)=12
Step 2: Calculate f′(0)
The derivative of a determinant is the sum of determinants obtained by differentiating one row (or column) at a time.
Let A(x)=(aij(x)). Then A′(x) is the sum of three determinants, where in each determinant, one row is replaced by its derivatives, and the other rows remain unchanged.
First, find the derivatives of each element: a11(x)=x3⟹a11′(x)=3x2 a12(x)=2x2+1⟹a12′(x)=4x a13(x)=1+3x⟹a13′(x)=3
a21(x)=3x2+2⟹a21′(x)=6x a22(x)=2x⟹a22′(x)=2 a23(x)=x3+6⟹a23′(x)=3x2
a31(x)=x3−x⟹a31′(x)=3x2−1 a32(x)=4⟹a32′(x)=0 a33(x)=x2−2⟹a33′(x)=2x
Now, evaluate the elements and their derivatives at x=0:
Original elements at x=0: Row 1: (0,1,1) Row 2: (2,0,6) Row 3: (0,4,−2)
Derivatives of elements at x=0: Row 1: (0,0,3) Row 2: (0,2,0) Row 3: (−1,0,0)
Now, form the three determinants for f′(0): f′(0)=a11′(0)a21(0)a31(0)a12′(0)a22(0)a32(0)a13′(0)a23(0)a33(0)+a11(0)a21′(0)a31(0)a12(0)a22′(0)a32(0)a13(0)a23′(0)a33(0)+a11(0)a21(0)a31′(0)a12(0)a22(0)a32′(0)a13(0)a23(0)a33′(0)
f′(0)=02000436−2+00012410−2+02−1100160
Calculate each determinant:
-
D1=02000436−2 Expand along R1: D1=3⋅2004=3⋅(2⋅4−0⋅0)=3⋅8=24
-
D2=00012410−2 Since the first column (C1) consists entirely of zeros, the determinant is 0. D2=0
-
D3=02−1100160 Expand along R3: D3=−1⋅1016−0⋅cofactor+0⋅cofactor D3=−1⋅(1⋅6−1⋅0)=−1⋅6=−6
Summing these determinants: f′(0)=D1+D2+D3=24+0+(−6)=18
Step 3: Calculate 2f(0)+f′(0)
Substitute the values of f(0) and f′(0): 2f(0)+f′(0)=2(12)+18=24+18=42
Therefore, the final answer is 42.
