Solveeit Logo
Login

Question

Question: $f(x) = sin^{-1}\sqrt{1-x^2}$...

f(x)=sin−11−x2f(x) = sin^{-1}\sqrt{1-x^2}

Answer

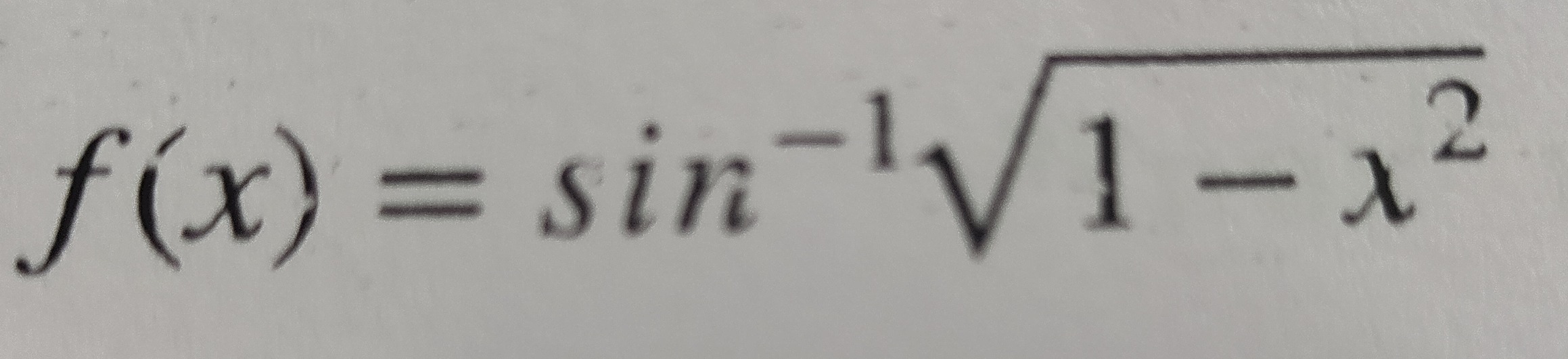
The domain of the function is [−1,1][-1, 1].

Explanation

Solution

The given function is f(x)=sin⁡−11−x2f(x) = \sin^{-1}\sqrt{1-x^2}.

To find the domain of the function, we need to ensure that the expressions inside the function are defined.

  1. The term inside the square root must be non-negative: 1−x2≥01-x^2 \ge 0.
    This inequality can be rewritten as x2≤1x^2 \le 1, which implies −1≤x≤1-1 \le x \le 1.

  2. The argument of the inverse sine function must be in the interval [−1,1][-1, 1]. The argument is 1−x2\sqrt{1-x^2}.
    So, we must have −1≤1−x2≤1-1 \le \sqrt{1-x^2} \le 1.
    Since the square root symbol ⋅\sqrt{\cdot} denotes the non-negative square root, 1−x2≥0\sqrt{1-x^2} \ge 0 is always true for real xx whenever 1−x2≥01-x^2 \ge 0. Thus, the condition −1≤1−x2-1 \le \sqrt{1-x^2} is automatically satisfied for the values of xx where 1−x2\sqrt{1-x^2} is defined.

The remaining condition is 1−x2≤1\sqrt{1-x^2} \le 1.
Since both sides are non-negative (as 1≥01 \ge 0 and 1−x2≥0\sqrt{1-x^2} \ge 0 when defined), we can square both sides without changing the inequality direction:
(1−x2)2≤12(\sqrt{1-x^2})^2 \le 1^2
1−x2≤11-x^2 \le 1
−x2≤0-x^2 \le 0
x2≥0x^2 \ge 0.
This inequality is true for all real numbers xx.

Combining the conditions for the domain:
From condition 1, we must have x∈[−1,1]x \in [-1, 1].
From condition 2, we must have x2≥0x^2 \ge 0, which is true for all real xx.
The intersection of these conditions is [−1,1][-1, 1].
Thus, the domain of the function f(x)=sin⁡−11−x2f(x) = \sin^{-1}\sqrt{1-x^2} is [−1,1][-1, 1].

To find the range of the function, we consider the values that f(x)f(x) can take for xx in its domain [−1,1][-1, 1].
Let y=f(x)=sin⁡−11−x2y = f(x) = \sin^{-1}\sqrt{1-x^2}.
As xx varies in the interval [−1,1][-1, 1], the value of x2x^2 varies in the interval [0,1][0, 1].
Then, 1−x21-x^2 varies in the interval [1−1,1−0]=[0,1][1-1, 1-0] = [0, 1].
The term 1−x2\sqrt{1-x^2} varies in the interval [0,1]=[0,1][\sqrt{0}, \sqrt{1}] = [0, 1].
So, the argument of the inverse sine function is in the interval [0,1][0, 1].
The range of sin⁡−1(u)\sin^{-1}(u) for u∈[0,1]u \in [0, 1] is [sin⁡−1(0),sin⁡−1(1)]=[0,π/2][\sin^{-1}(0), \sin^{-1}(1)] = [0, \pi/2].
Therefore, the range of f(x)=sin⁡−11−x2f(x) = \sin^{-1}\sqrt{1-x^2} is [0,π/2][0, \pi/2].

The function can also be simplified. Let x=cos⁡θx = \cos\theta. Since x∈[−1,1]x \in [-1, 1], we can choose θ∈[0,π]\theta \in [0, \pi].
Then 1−x2=1−cos⁡2θ=sin⁡2θ=∣sin⁡θ∣\sqrt{1-x^2} = \sqrt{1-\cos^2\theta} = \sqrt{\sin^2\theta} = |\sin\theta|.
Since θ∈[0,π]\theta \in [0, \pi], sin⁡θ≥0\sin\theta \ge 0, so ∣sin⁡θ∣=sin⁡θ|\sin\theta| = \sin\theta.
Thus, f(x)=sin⁡−1(sin⁡θ)f(x) = \sin^{-1}(\sin\theta).
For θ∈[0,π]\theta \in [0, \pi], sin⁡−1(sin⁡θ)={θif θ∈[0,π/2]π−θif θ∈(π/2,π]\sin^{-1}(\sin\theta) = \begin{cases} \theta & \text{if } \theta \in [0, \pi/2] \\ \pi-\theta & \text{if } \theta \in (\pi/2, \pi] \end{cases}.
If θ∈[0,π/2]\theta \in [0, \pi/2], then x=cos⁡θ∈[cos⁡(π/2),cos⁡(0)]=[0,1]x = \cos\theta \in [\cos(\pi/2), \cos(0)] = [0, 1]. In this case, f(x)=θ=cos⁡−1xf(x) = \theta = \cos^{-1}x.
If θ∈(π/2,π]\theta \in (\pi/2, \pi], then x=cos⁡θ∈[cos⁡(π),cos⁡(π/2))=[−1,0)x = \cos\theta \in [\cos(\pi), \cos(\pi/2)) = [-1, 0). In this case, f(x)=π−θ=π−cos⁡−1xf(x) = \pi-\theta = \pi-\cos^{-1}x.
Using the identity π−cos⁡−1x=cos⁡−1(−x)=cos⁡−1∣x∣\pi-\cos^{-1}x = \cos^{-1}(-x) = \cos^{-1}|x| for x∈[−1,0)x \in [-1, 0), and cos⁡−1x=cos⁡−1∣x∣\cos^{-1}x = \cos^{-1}|x| for x∈[0,1]x \in [0, 1], we get the simplified form f(x)=cos⁡−1∣x∣f(x) = \cos^{-1}|x| for x∈[−1,1]x \in [-1, 1].

The domain is [−1,1][-1, 1].
The range is [0,π/2][0, \pi/2].

The question asks for the function f(x)f(x). Without a specific question (like find the domain, range, or simplify), we provide the domain as it's a fundamental property.