Question

f(x) = ln|\frac{sin^{2025}x-1}{sin^{2025}x+1}|

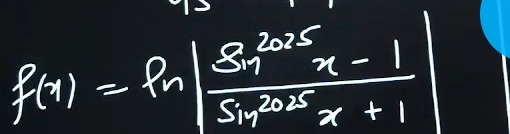
Answer 1

The function can be simplified to: $f(x) = \ln\left(\frac{1-\sin^{2025}x}{1+\sin^{2025}x}\right)$

The domain of the function is all real numbers $x$ such that $x \neq \frac{\pi}{2} + n\pi$, where $n$ is an integer.

Answer 2

The domain requires the argument of the logarithm to be positive: $\left|\frac{\sin^{2025}x-1}{\sin^{2025}x+1}\right| > 0$. This implies $\sin^{2025}x \neq 1$ and $\sin^{2025}x \neq -1$, leading to $-1 < \sin x < 1$, so $x \neq \frac{\pi}{2} + n\pi$. For $-1 < \sin^{2025}x < 1$, the term $\frac{\sin^{2025}x-1}{\sin^{2025}x+1}$ is negative. Thus, its absolute value is $-\left(\frac{\sin^{2025}x-1}{\sin^{2025}x+1}\right) = \frac{1-\sin^{2025}x}{1+\sin^{2025}x}$. Therefore, $f(x) = \ln\left(\frac{1-\sin^{2025}x}{1+\sin^{2025}x}\right)$.