Question
Question: Determine the range of the function $f(x) = \frac{2025^{\tan x}}{45^{\tan x}+1}$....
Determine the range of the function f(x)=45tanx+12025tanx.
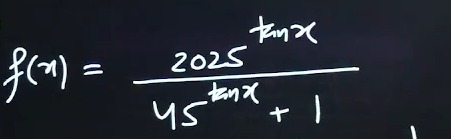
(0, \infty)
Solution
To determine the range of the function f(x)=45tanx+12025tanx, we can follow these steps:
-
Simplify the expression: Notice that 2025=452. Substitute this into the function: f(x)=45tanx+1(452)tanx=45tanx+1(45tanx)2
-
Introduce a substitution: Let u=45tanx. The function then becomes a function of u: g(u)=u+1u2
-
Determine the domain of the substituted variable u: The domain of tanx is all real numbers, R. Since the base 45>0, the exponential function 45y always produces positive values. Therefore, the range of u=45tanx is (0,∞). We need to find the range of g(u) for u∈(0,∞).
-
Analyze the function g(u) for its range: We can analyze the behavior of g(u) by considering its derivative: g′(u)=dud(u+1u2) Using the quotient rule, g′(u)=(u+1)2(2u)(u+1)−(u2)(1)=(u+1)22u2+2u−u2=(u+1)2u2+2u=(u+1)2u(u+2).
For u∈(0,∞):
- u>0
- u+2>0
- (u+1)2>0 Therefore, g′(u)>0 for all u∈(0,∞). This indicates that g(u) is strictly increasing on its domain (0,∞).
Now, we evaluate the limits of g(u) as u approaches the boundaries of its domain:
- As u→0+: limu→0+g(u)=limu→0+u+1u2=0+102=0
- As u→∞: limu→∞g(u)=limu→∞u+1u2 We can divide the numerator and denominator by u: limu→∞1+u1u=1+0∞=∞
Since g(u) is strictly increasing on (0,∞) and its limits at the boundaries are 0 and ∞, the range of g(u) for u∈(0,∞) is (0,∞).
Therefore, the range of the function f(x) is (0,∞).
