Question

$f(x) = \frac{1}{x}log(\frac{1+3x}{1-2x})$ when $x \neq 0$ and $f(0) = k$. The value of $k$ so that $f(x)$ is continuous at $x = 0$

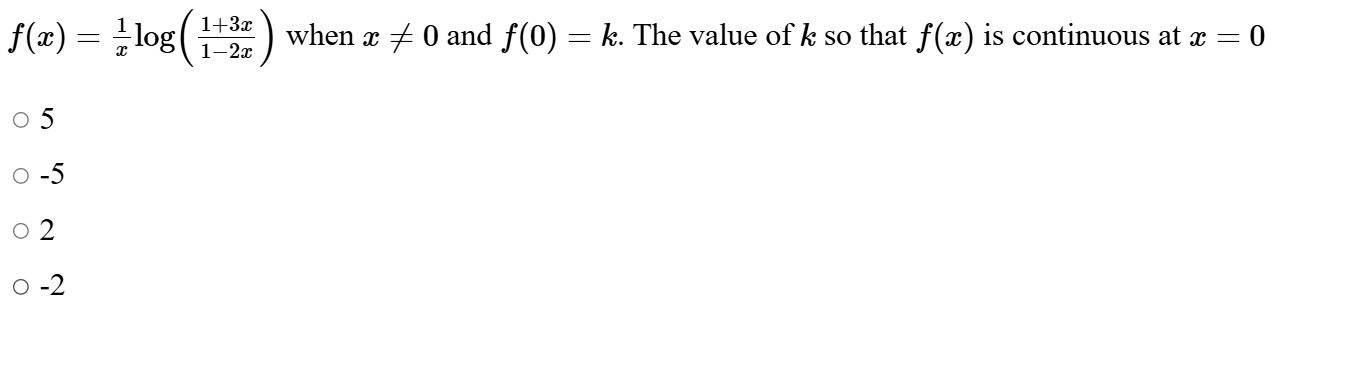
• A. 5
• B. -5
• C. 2
• D. -2

Answer 1

Answer: (A)

5

Answer 2

For $f(x)$ to be continuous at $x=0$, the limit of $f(x)$ as $x$ approaches $0$ must be equal to $f(0)$. Given $f(x) = \frac{1}{x}\log\left(\frac{1+3x}{1-2x}\right)$ for $x \neq 0$, and $f(0) = k$. Thus, we need to find $k$ such that: $k = \lim_{x \to 0} \frac{1}{x}\log\left(\frac{1+3x}{1-2x}\right)$

Using the property of logarithms, $\log\left(\frac{a}{b}\right) = \log a - \log b$: $k = \lim_{x \to 0} \frac{\log(1+3x) - \log(1-2x)}{x}$

We can split this into two separate limits: $k = \lim_{x \to 0} \frac{\log(1+3x)}{x} - \lim_{x \to 0} \frac{\log(1-2x)}{x}$

We use the standard limit: $\lim_{u \to 0} \frac{\log(1+u)}{u} = 1$.

For the first term: $\lim_{x \to 0} \frac{\log(1+3x)}{x} = \lim_{x \to 0} 3 \cdot \frac{\log(1+3x)}{3x}$ Let $y = 3x$. As $x \to 0$, $y \to 0$. $3 \lim_{y \to 0} \frac{\log(1+y)}{y} = 3 \cdot 1 = 3$.

For the second term: $\lim_{x \to 0} \frac{\log(1-2x)}{x} = \lim_{x \to 0} (-2) \cdot \frac{\log(1-2x)}{-2x}$ Let $z = -2x$. As $x \to 0$, $z \to 0$. $-2 \lim_{z \to 0} \frac{\log(1+z)}{z} = -2 \cdot 1 = -2$.

Substituting these values back: $k = 3 - (-2) = 3 + 2 = 5$.

Therefore, the value of $k$ that makes $f(x)$ continuous at $x=0$ is 5.