Question

$f(x) = ax^{17} + b \sin x \cdot \sin 2x \cdot \sin 3x + cx^2 sgn(\sin x) + d \log{(x + \sqrt{1 + x^2})} + x(|x + 1| - |x - 1|)\left(\frac{e^x - e^{-x}}{e^x + e^{-x}}\right)$

be defined on the set of real numbers, $(a > 0, b, c, d \in R)$ if $f(-7) = 7, f(-5) = -5, f(-2) = 3$, then the minimum number of zeroes of the equation $f(x) = 0$ is equal to ___.

Answer 1

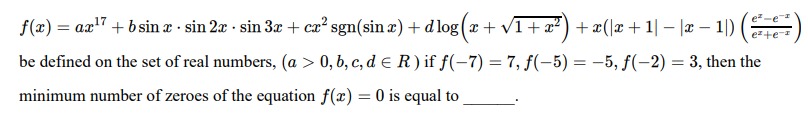
5

Answer 2

The given function is $f(x) = ax^{17} + b \sin x \cdot \sin 2x \cdot \sin 3x + cx^2 sgn(\sin x) + d \log{(x + \sqrt{1 + x^2})} + x(|x + 1| - |x - 1|)\left(\frac{e^x - e^{-x}}{e^x + e^{-x}}\right)$.

Let's analyze the parity of each term:

1. $ax^{17}$: This is an odd function since $(-x)^{17} = -x^{17}$.
2. $b \sin x \cdot \sin 2x \cdot \sin 3x$: $\sin(-x) = -\sin x$, $\sin(-2x) = -\sin 2x$, $\sin(-3x) = -\sin 3x$. So, $b \sin(-x) \sin(-2x) \sin(-3x) = b (-\sin x) (-\sin 2x) (-\sin 3x) = -b \sin x \sin 2x \sin 3x$. This is an odd function.
3. $cx^2 sgn(\sin x)$: $(-x)^2 = x^2$. $sgn(\sin(-x)) = sgn(-\sin x)$. We know $sgn(-y) = -sgn(y)$. So, $sgn(\sin(-x)) = -sgn(\sin x)$. Thus, $c(-x)^2 sgn(\sin(-x)) = cx^2 (-sgn(\sin x)) = -cx^2 sgn(\sin x)$. This is an odd function.
4. $d \log{(x + \sqrt{1 + x^2})}$: Let $g(x) = \log{(x + \sqrt{1 + x^2})}$. $g(-x) = \log{(-x + \sqrt{1 + (-x)^2})} = \log{(-x + \sqrt{1 + x^2})}$. We can write $-x + \sqrt{1 + x^2} = \frac{(\sqrt{1+x^2}-x)(\sqrt{1+x^2}+x)}{\sqrt{1+x^2}+x} = \frac{1+x^2-x^2}{\sqrt{1+x^2}+x} = \frac{1}{x + \sqrt{1 + x^2}}$. So, $g(-x) = \log{\left(\frac{1}{x + \sqrt{1 + x^2}}\right)} = -\log{(x + \sqrt{1 + x^2})} = -g(x)$. This is an odd function.
5. $x(|x + 1| - |x - 1|)\left(\frac{e^x - e^{-x}}{e^x + e^{-x}}\right)$: Let $h_1(x) = |x + 1| - |x - 1|$. $h_1(-x) = |-x + 1| - |-x - 1| = |x - 1| - |x + 1| = -(|x + 1| - |x - 1|) = -h_1(x)$. So $h_1(x)$ is an odd function. Let $h_2(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \tanh x$. $h_2(-x) = \tanh(-x) = -\tanh x = -h_2(x)$. So $h_2(x)$ is an odd function. The term is $x \cdot h_1(x) \cdot h_2(x)$. This is (odd) $\cdot$ (odd) $\cdot$ (odd) = (even) $\cdot$ (odd) = odd. So, the entire fifth term is an odd function.

Since all individual terms are odd functions, their sum $f(x)$ is an odd function. This means $f(-x) = -f(x)$ for all $x \in R$. For an odd function, if $f(0)$ is defined, then $f(0) = -f(0) \implies 2f(0) = 0 \implies f(0) = 0$. Let's check $f(0)$: $f(0) = a(0)^{17} + b \sin 0 \cdot \sin 0 \cdot \sin 0 + c(0)^2 sgn(\sin 0) + d \log{(0 + \sqrt{1 + 0^2})} + 0(|0 + 1| - |0 - 1|)\left(\frac{e^0 - e^{-0}}{e^0 + e^{-0}}\right)$ $f(0) = 0 + 0 + 0 + d \log(1) + 0 = 0$. So, $x=0$ is a zero of $f(x)$.

We are given the following values: $f(-7) = 7$ $f(-5) = -5$ $f(-2) = 3$

Using the property $f(-x) = -f(x)$: $f(7) = -f(-7) = -7$ $f(5) = -f(-5) = -(-5) = 5$ $f(2) = -f(-2) = -3$

Now we have the following points for $f(x)$: $f(-7) = 7$ $f(-5) = -5$ $f(-2) = 3$ $f(0) = 0$ $f(2) = -3$ $f(5) = 5$ $f(7) = -7$

Next, we need to check the continuity of $f(x)$. All terms are continuous except potentially $cx^2 sgn(\sin x)$. The function $sgn(\sin x)$ is discontinuous at $x = n\pi$ for $n \in Z$. However, the term is $cx^2 sgn(\sin x)$. At $x=n\pi$, $f_3(n\pi) = c(n\pi)^2 sgn(\sin(n\pi)) = c(n\pi)^2 \cdot 0 = 0$. Consider $x \to n\pi$. If $n$ is an even integer (e.g., $x \to 2k\pi$), $\sin x$ changes from negative to positive. $\lim_{x \to (2k\pi)^-} cx^2 sgn(\sin x) = c(2k\pi)^2 (-1) = -c(2k\pi)^2$. $\lim_{x \to (2k\pi)^+} cx^2 sgn(\sin x) = c(2k\pi)^2 (1) = c(2k\pi)^2$. For continuity, these limits must be equal to $f_3(2k\pi) = 0$. This implies $-c(2k\pi)^2 = c(2k\pi)^2 = 0$, which means $c=0$ (for $k \ne 0$). If $n$ is an odd integer (e.g., $x \to (2k+1)\pi$), $\sin x$ changes from positive to negative. $\lim_{x \to ((2k+1)\pi)^-} cx^2 sgn(\sin x) = c((2k+1)\pi)^2 (1) = c((2k+1)\pi)^2$. $\lim_{x \to ((2k+1)\pi)^+} cx^2 sgn(\sin x) = c((2k+1)\pi)^2 (-1) = -c((2k+1)\pi)^2$. For continuity, these limits must be equal to $f_3((2k+1)\pi) = 0$. This implies $c((2k+1)\pi)^2 = -c((2k+1)\pi)^2 = 0$, which means $c=0$. So, $f(x)$ is continuous only if $c=0$. If $c \ne 0$, $f(x)$ is discontinuous at $x = n\pi$ for $n \ne 0$.

The values of $x$ for which $f(x)$ is given are $-7, -5, -2, 0, 2, 5, 7$. None of these are multiples of $\pi$ except $0$. The multiples of $\pi$ between $-7$ and $7$ are $-2\pi \approx -6.28$, $-\pi \approx -3.14$, $0$, $\pi \approx 3.14$, $2\pi \approx 6.28$.

Let's evaluate $f(n\pi)$ for $n \ne 0$: $f(n\pi) = a(n\pi)^{17} + b \cdot 0 + c \cdot 0 + d \log(n\pi + \sqrt{1+(n\pi)^2}) + n\pi(|n\pi+1|-|n\pi-1|)\tanh(n\pi)$. For $n=1$, $f(\pi) = a\pi^{17} + d \log(\pi + \sqrt{1+\pi^2}) + \pi((\pi+1)-(\pi-1))\tanh(\pi) = a\pi^{17} + d \log(\pi + \sqrt{1+\pi^2}) + 2\pi \tanh(\pi)$. Since $a>0$, $a\pi^{17} > 0$. $\log(\pi + \sqrt{1+\pi^2}) > 0$. $\tanh(\pi) > 0$. So, $f(\pi)$ is likely positive (unless $d$ is sufficiently negative). Similarly, $f(2\pi) = a(2\pi)^{17} + d \log(2\pi + \sqrt{1+(2\pi)^2}) + 2\pi((2\pi+1)-(2\pi-1))\tanh(2\pi) = a(2\pi)^{17} + d \log(2\pi + \sqrt{1+(2\pi)^2}) + 4\pi \tanh(2\pi)$. $f(2\pi)$ is also likely positive. Since $f(x)$ is an odd function, $f(-\pi) = -f(\pi)$ and $f(-2\pi) = -f(2\pi)$. So $f(-\pi)$ and $f(-2\pi)$ are likely negative.

Let's analyze the signs of $f(x)$ values: $f(-7) = 7 \quad (>0)$ $f(-2\pi) \quad (<0)$ (assuming $f(2\pi)>0$) $f(-5) = -5 \quad (<0)$ $f(-\pi) \quad (<0)$ (assuming $f(\pi)>0$) $f(-2) = 3 \quad (>0)$ $f(0) = 0 \quad (=0)$ $f(2) = -3 \quad (<0)$ $f(\pi) \quad (>0)$ $f(5) = 5 \quad (>0)$ $f(2\pi) \quad (>0)$ $f(7) = -7 \quad (<0)$

We use the Intermediate Value Theorem (IVT) on intervals where $f(x)$ is continuous and changes sign. The minimum number of zeroes is guaranteed by IVT.

1. In the interval $(-7, -2\pi)$: $f(-7) = 7 > 0$ and $f(-2\pi) < 0$. Since $f(x)$ is continuous on $(-7, -2\pi)$, there must be at least one zero in $(-7, -2\pi)$.
2. In the interval $(-\pi, -2)$: $f(-\pi) < 0$ and $f(-2) = 3 > 0$. Since $f(x)$ is continuous on $(-\pi, -2)$, there must be at least one zero in $(-\pi, -2)$.
3. At $x=0$: $f(0) = 0$. This is a guaranteed zero.
4. In the interval $(2, \pi)$: $f(2) = -3 < 0$ and $f(\pi) > 0$. Since $f(x)$ is continuous on $(2, \pi)$, there must be at least one zero in $(2, \pi)$.
5. In the interval $(2\pi, 7)$: $f(2\pi) > 0$ and $f(7) = -7 < 0$. Since $f(x)$ is continuous on $(2\pi, 7)$, there must be at least one zero in $(2\pi, 7)$.

These 5 zeroes are distinct and guaranteed regardless of the value of $c$ (as long as $c$ is a real number, if $c=0$ then function is continuous everywhere and these zeroes exist as well). The problem asks for the minimum number of zeroes, so we assume the most general case (that $f(n\pi) \ne 0$ for $n \ne 0$). If $f(n\pi)$ happens to be zero for some $n \ne 0$, it would only add more zeroes, not reduce the minimum count.

Thus, the minimum number of zeroes of the equation $f(x)=0$ is 5.

Explanation of the solution:

1. Analyze the parity of each term in $f(x)$. All terms are found to be odd functions. Therefore, $f(x)$ is an odd function, meaning $f(-x) = -f(x)$.
2. Use the given values $f(-7)=7, f(-5)=-5, f(-2)=3$ to find $f(7)=-7, f(5)=5, f(2)=-3$.
3. For an odd function, if defined at $x=0$, $f(0)=0$. Verify that $f(0)=0$. This gives one zero.
4. Identify potential points of discontinuity for $f(x)$. The term $cx^2 sgn(\sin x)$ makes $f(x)$ discontinuous at $x=n\pi$ for $n \in Z, n \ne 0$, unless $c=0$.
5. Evaluate the sign of $f(x)$ at the given points and the discontinuity points ($n\pi$). Assuming $f(n\pi) \ne 0$ for $n \ne 0$ (which represents the minimum case). $f(-7)>0$, $f(-2\pi)<0$, $f(-5)<0$, $f(-\pi)<0$, $f(-2)>0$, $f(0)=0$, $f(2)<0$, $f(\pi)>0$, $f(5)>0$, $f(2\pi)>0$, $f(7)<0$.
6. Apply the Intermediate Value Theorem (IVT) to the continuous segments of $f(x)$ where the sign changes.
   • One zero in $(-7, -2\pi)$ because $f(-7)>0$ and $f(-2\pi)<0$.
   • One zero in $(-\pi, -2)$ because $f(-\pi)<0$ and $f(-2)>0$.
   • One zero at $x=0$ because $f(0)=0$.
   • One zero in $(2, \pi)$ because $f(2)<0$ and $f(\pi)>0$.
   • One zero in $(2\pi, 7)$ because $f(2\pi)>0$ and $f(7)<0$.
7. These 5 zeroes are distinct and guaranteed, providing the minimum number of zeroes for $f(x)=0$.

Answer: 5