Question

From the top of a lighthouse, the angle of the depression of two ships on the opposite side of it are observed to be $\alpha$and $\beta .$If the height of the light house be $h$ meters and the line joining the ships passes through the foot of the light house, show that the distance between the ships is $\dfrac{{h(\tan \alpha + \tan \beta )}}{{\tan \alpha \tan \beta }}meters.$

Answer 1

To solve such problems. First draw a correct diagram taking ships as points and the lighthouse as a perpendicular line. Then convert the word problem into mathematical equations to solve the question. Use triangle properties of trigonometric ratios.

Complete step by step solution:
First, let us draw the diagram, explaining the question.

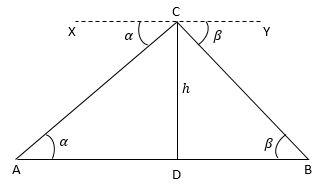
Let, A and B be two boats.
CD be the light house
$\angle XCA = \alpha$and $\angle YCB = \beta$ be the angles of depression from the top of the light house to the boats A and B respectively.
We need to prove that the distance, AB between the ships is equal to $\dfrac{{h(\tan \alpha + \tan \beta )}}{{\tan \alpha \tan \beta }}meters.$
Since $XY||AB,$by using the property of alternate interior angles, we can say that
$\angle XCA = \angle CAD = \alpha$and $\angle YCB = \angle CBD = \beta$
Now, in $\Delta ACD$
$\tan \alpha = \dfrac{h}{{AD}}$
Rearranging it, we can write
$AD = \dfrac{h}{{\tan \alpha }}$ . . . (1)
Similarly, In $\Delta BCD$
$\tan \beta = \dfrac{h}{{BD}}$
$\Rightarrow BD = \dfrac{h}{{\tan \beta }}$ . . . (2)
We know that the distance between the ships,
$AB = AD + DB$
Adding equation (1) and equation (2), we get
$AB = AD + BD = \dfrac{h}{{\tan \alpha }} + \dfrac{h}{{\tan \beta }}$
By taking $h$common, we get
$AB = h\left( {\dfrac{1}{{\tan \alpha }} + \dfrac{1}{{\tan \beta }}} \right)meter$
By cross multiplying the terms, we can simplify it to
$AB = \dfrac{{h(\tan \beta + \tan \alpha )}}{{\tan \alpha \tan \beta }}meter$
Hence, it is proved that the distance between the ships is $\dfrac{{h(\tan \alpha + \tan \beta )}}{{\tan \alpha \tan \beta }}$ meters

Note: To speed up the calculation in the future, you can remember the fact that the angle of elevation and the angle of depression are always equal. Since, it was not given in the question that the ships are at the equal distance from the lighthouse, we did not assume $AD = BD.$ You should keep this in mind to not assume something that is not given in the question.