Question

From the top of a cliff $20m$ high, the angle of elevation of the top of a tower is found to be equal to the angle of depression of the foot of a tower. Find the height of the tower.

Answer 1

The question belongs to the topic- heights and distances. In such questions, trigonometric ratios are used to find the required length or distance. Start by making a figure as per the question. Mark all the angles and lengths given. Find a relation between the given side and the side to be found. Using the relation between the two sides, use a suitable trigonometric ratio.

Complete step-by-step answer:
Start by making a diagram as per the question. Let CH be the cliff, AD be the tower whose length is to be found. We are given $CH = 20m$. We can see

$BD = CH = 20m$.
It is given that the two angles- one to the top of the tower and other to the bottom of the tower- are equal. Let $\angle ACB = \angle BCD = x^\circ$.
In $\vartriangle BCD$,
$\Rightarrow \tan x^\circ = \dfrac{{BD}}{{BC}}$
Putting $BD = 20m$,
$\Rightarrow \tan x^\circ = \dfrac{{20}}{{BC}}$ …..…. (1)
In $\vartriangle ABC$,
$\Rightarrow \tan x^\circ = \dfrac{{AB}}{{BC}}$ ….…. (2)
Since LHS of equations (1) and (2) are same, we will equate them-
$\Rightarrow \dfrac{{20}}{{BC}} = \dfrac{{AB}}{{BC}}$
Shifting and solving,
$\Rightarrow \dfrac{{20}}{{AB}} = \dfrac{{BC}}{{BC}}$
$\Rightarrow \dfrac{{20}}{{AB}} = 1$
$\Rightarrow AB = 20m$
Now, we know that tower = $AB + BD$ $= 20m + 20m = 40m$

Hence, the height of the tower is $40m$.

Note: There are certain terms used in the question which are important to understand before solving any heights and distances question-

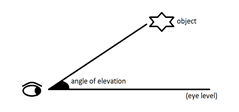
1. Angle of elevation: It is the angle formed when we see an object above our eye level.
   
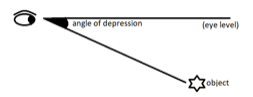
2. Angle of depression: It is an angle formed when we see an object below our eye level.