Question

From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be $30^\circ$ and $60^\circ$ respectively. Find the difference between the heights of the building and the lamp post.

Answer 1

Here, we will use the properties of trigonometric functions in a triangle and then apply the given condition to find two different equations. Solving these equations, we will get the height of the vertical lamp post. We will subtract the height of the lamppost from the height of the building to get the required answer.

Formula used: We will use the formula $\tan \theta = \dfrac{P}{B}$, where $P$ is the perpendicular side and $B$ is the base.

Complete step-by-step answer:
Let AB be a building of height 60 m.
Let CD be a vertical lamp pole with the base C and the top D of height $h$ m.
It is given that the angles of depression of the top and bottom of a vertical lamp post CD are observed to be $30^\circ$ and $60^\circ$ respectively.
Hence, we will draw a figure showing these angles of depression such that $\angle BDE = 30^\circ$ and $\angle BCA = 60^\circ$.

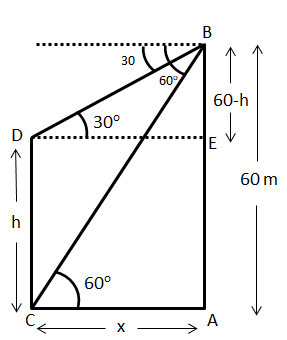
Now, from the figure $AB = 60{\rm{m}}$ and $CD = h$.
Therefore, $BE = \left( {60 - h} \right){\rm{m}}$
Also, let the distance between the building and the vertical lamp pole be $x$. So,
$AC = x$
Now, in $\Delta DEB$,
$\tan 30^\circ = \dfrac{{BE}}{{DE}}$
Substituting the value of the trigonometric function $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ in the above equation, we get
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{BE}}{{DE}}$
The line DE is parallel to the base AC , so DE is equal to $x$ meters.
Substituting $BE = \left( {60 - h} \right)$ and $DE = x$ in the above equation, we get
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{60 - h}}{x}$
Hence, solving further by doing cross multiplication, we get
$x = \sqrt 3 \left( {60 - h} \right)$………………………………$\left( 1 \right)$
Now, again, in $\Delta CAB$,
$\tan 60^\circ = \dfrac{{AB}}{{AC}}$
Substituting the value of the trigonometric function $\tan 60^\circ = \sqrt 3$ in above equation, we get
$\Rightarrow \tan 60^\circ = \sqrt 3 = \dfrac{{60}}{x}$
Hence, solving further by doing cross multiplication, we get
$x = \dfrac{{60}}{{\sqrt 3 }}$………………………………$\left( 2 \right)$
Now, equating the values of $x$ from $\left( 1 \right)$ and $\left( 2 \right)$, we get
$\sqrt 3 \left( {60 - h} \right) = \dfrac{{60}}{{\sqrt 3 }}$
Multiplying both sides by $\sqrt 3$, we get
$\Rightarrow 3\left( {60 - h} \right) = 60$
Dividing both sides by 3, we get
$\Rightarrow \left( {60 - h} \right) = 20$
Adding $h - 20$ on both sides, we get
$\Rightarrow h = 60 - 20 = 40{\rm{m}}$
Hence, the height of the vertical lamp post $= h = 40{\rm{m}}$
Also, the height of the building is 60 m.
Therefore, the difference between the heights of the building and the lamp post $= 60 - 40 = 20{\rm{m}}$
Hence, this is the required answer.

Note: In the applications of trigonometry, to show the angle of depression, we draw an imaginary line of sight which is always parallel to the base. The angle between that imaginary line of sight and the line joining the object is called the angle of depression. The angle of depression is always below the line of sight, whereas, the angle of elevation is always above the baseline. The angle of elevation and the angle of depression are actually congruent to each other.