Question

From the top of a building 60m high the angle of depression of the top and the bottom of a tower are observed to be ${{30}^{\circ }}$ and ${{60}^{\circ }}$. Find the height of the tower.
A. 60m
B. 40m
C. 80m
D. 70m

Answer 1

Hint: Draw the figure as per mentioned in the question. We have been given the angle of depression from the top of the building to the top and bottom of the lamp post. Thus find the height of lamp pose with the triangles formed.

Complete step by step answer:
Let us consider the CD as the height of the lamp, from the figure.

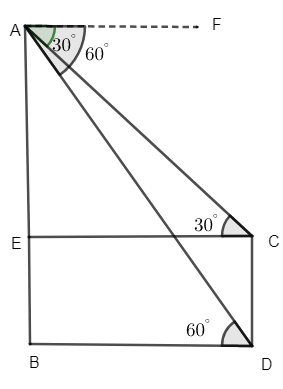
Let AB be the height of the building.
From the top of building AB, the angle of depression of the top and bottom of the tower CD is ${{30}^{\circ }}$ and ${{60}^{\circ }}$.
From the figure we can understand that the ground level BD is parallel to the lamp CE.
Thus we can say that BD || CE.
So we can say that, $\angle FAC=\angle ACE={{30}^{\circ }}$ i.e. they are alternate angles.
Similarly, $\angle FAD=\angle ADB={{60}^{\circ }}$, alternate angles.
Now from the figure, let us consider $\Delta AEC$.
We know $\tan {{30}^{\circ }}$ =$\dfrac{opposite side} { adjacent side}$ = $\dfrac{AE}{CE}$.
From the trigonometric table, $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$.

& \therefore \dfrac{1}{\sqrt{3}}=\dfrac{AE}{CE} \\\ & \therefore CE=\sqrt{3}AE-(1) \\\ \end{aligned}$$ Now let us consider $$\Delta ABD$$. $$\tan {{60}^{\circ }}$$ = $$\dfrac{opposite side} { adjacent side}$$=$$\dfrac{AB}{BD}$$ From the trigonometric table, $$\tan {{60}^{\circ }}=\sqrt{3}$$. $$\therefore \sqrt{3}=\dfrac{AB}{BD}\Rightarrow AB=BD\sqrt{3}$$ As BD || CE, we can say that, BD = CE. $$\therefore AB=\sqrt{3}CE-(2)$$ $$CE=\dfrac{AB}{\sqrt{3}}$$ and $$CE=\sqrt{3}AE$$. $$\begin{aligned} & \therefore \sqrt{3}AE=\dfrac{AB}{\sqrt{3}} \\\ & \therefore AB=3AE \\\ \end{aligned}$$ We know, AB = 60m. $$\therefore 60=3AE$$ $$\Rightarrow AE=\dfrac{60}{3}=20$$m. Thus we got AE = 20m. $$\therefore CE=\sqrt{3}AE=20\sqrt{3}$$m. Where, CE = BD = $$20\sqrt{3}$$, it is the distance between the building and the lamp post. We know from figure that, AB = AE + BE Where, BE = CD = height of the lamp. $$\therefore $$ AB = AE + CD AB = 60m, AE = 20m, thus find CD $$\Rightarrow 60=20+CD$$ CD = 60 – 20 = 40m. Thus the height of the lamp = 40m. $$\therefore $$ Option (B) is the correct answer. Note: The angles given are the angle of depression. Then as the ground is parallel to the height of the lamp post we can convert the angle of depression to angle of elevation so as to make calculations easier i.e. they become alternate angles.