Question

From the top of a building $50\sqrt 3 m$ high, the angle of depression of an object on the ground is observed to be $45^\circ .$ Find the distance of the object from the building.

Answer 1

Hint : Convert the word problem into mathematical equations. Use trigonometric ratios to solve it. If we observe its Isosceles right angle triangle and the value of tan45 is 1.

Complete step-by-step answer :
Let us consider the building as $AB$, and consider the object as $C$

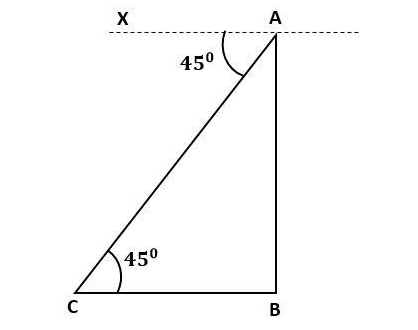
It is given that, angle of depression is ${45^0}$
$\Rightarrow \angle XAC = {45^0}$
Since, alternate interior angles of two parallel lines are equal, we get
$\angle ACB = {45^0}$ $\left( {\because AX||BC} \right)$
It is given that, the height of the building, $AB = 50\sqrt 3 m$
Now, in a $\Delta ABC$
$\tan C = \dfrac{{AB}}{{BC}}$
$\Rightarrow \tan {45^0} = \dfrac{{50\sqrt 3 }}{{BC}}$ $\left( {\because AB = 50\sqrt 3 m} \right)$
$\Rightarrow 1 = \dfrac{{50\sqrt 3 }}{{BC}}$ $\left( {\because \tan {{45}^0} = 1} \right)$
By cross multiplying, we get
$BC = 50\sqrt 3 m$
Therefore, the distance of object from the building is $50\sqrt 3 m$

Note : It can also be solved in short. A right angled triangle, whose one angle is ${45^0}$ must be isosceles triangle.
$\Rightarrow AB = BC = 50\sqrt 3 m$