Question

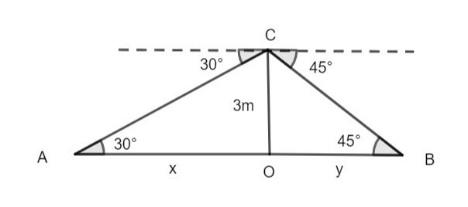
From the point on a bridge across a river, the angles of depressions of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
(a). $3(\sqrt 3 - 1)m$
(b). $3(\sqrt 3 + 1)m$
(c). $(3 + \sqrt 3 )m$
(d). $(3 - \sqrt 3 )m$

Answer 1

Hint: Consider the distance of bank A from the bridge be x and the distance of bank B from the bridge be y. Use the trigonometric ratio i.e tangent formula $\tan \theta = \dfrac{{{\text{Opposite Side}}}}{{{\text{Adjacent Side}}}}$ to find the distance of the bridge from the banks on either side and add them to get the final answer.

Complete step-by-step answer:
It is given that from a point on a bridge that is built across a river, the angles of depressions of the banks on opposite sides of the river are 30° and 45° respectively as shown in the figure and the height of the bridge is given as 3 m.
Let the distance of bank A from the bridge be x and the distance of bank B from the bridge be y.

We know the formula for the tangent of an angle of a triangle is given as follows:
$\tan \theta = \dfrac{{{\text{Opposite Side}}}}{{{\text{Adjacent Side}}}}$
In triangle AOC, angle CAO is given as 30°, using the tangent formula, we have:
$\tan 30^\circ = \dfrac{{\text{3}}}{x}$
We know that the value of $\tan 30^\circ$ is $\dfrac{1}{{\sqrt 3 }}$. Hence, we have:
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{\text{3}}}{x}$
$x = 3\sqrt 3 ............(1)$
In triangle BOC, angle CBO is given as 45°, using the tangent formula, we have:
$\tan 45^\circ = \dfrac{{\text{3}}}{y}$
We know that the value of $\tan 45^\circ$ is 1. Hence, we have:
$1 = \dfrac{{\text{3}}}{y}$
$y = 3............(2)$
The width of the river is the sum of the equations (1) and (2).
$AB = 3\sqrt 3 + 3$
$AB = 3(\sqrt 3 + 1)m$
Hence, the correct answer is option (b).

Note: The term angle of elevation denotes the angle from the horizontal upward to an object. An observer's line of sight would be above the horizontal. The term angle of depression denotes the angle from the horizontal downward to an object. An observer's line of sight would be below the horizontal. Student should know the trigonometric ratios and identities for solving these types of problems