Question

From the phase diagram of water and an aqueous solution containing non volatile solute, identify the correct options:

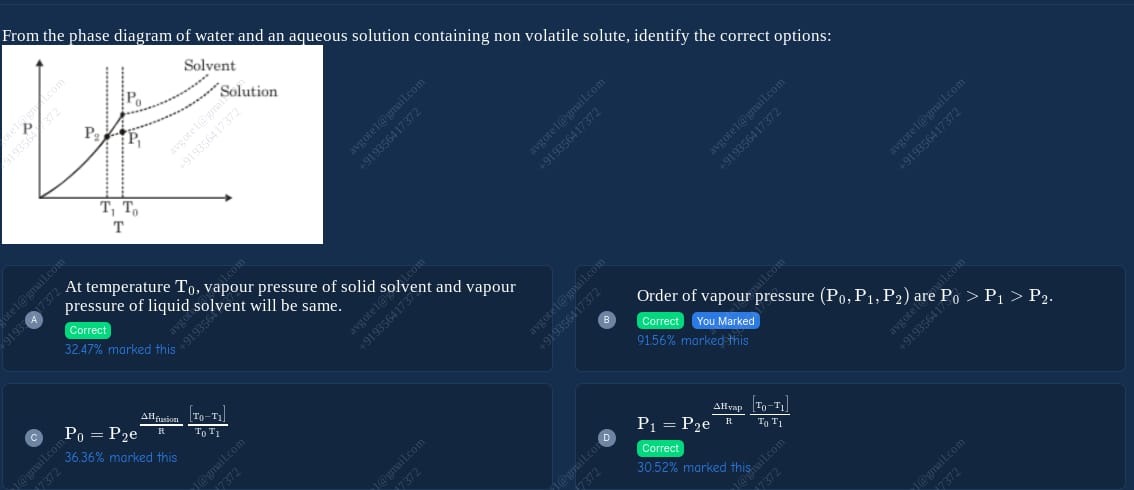
• A. At temperature $T_0$, vapour pressure of solid solvent and vapour pressure of liquid solvent will be same.
• B. Order of vapour pressure ($P_0, P_1, P_2$) are $P_0 > P_1 > P_2$.
• C. $P_0 = P_2e^{\frac{\Delta H_{fusion}}{R}[\frac{T_0 - T_1}{T_0 T_1}]}$
• D. $P_1 = P_2e^{\frac{\Delta H_{vap}}{R}[\frac{T_0 - T_1}{T_0 T_1}]}$

Answer 1

Answer: (A), (B), (C), (D)

All options A, B, C, and D are correct.

Answer 2

1. Option A: For a pure solvent, at its triple point (which occurs at $T_0$), the vapor pressures of the solid and liquid phases are equal. Hence option A is correct.

2. Option B: In the diagram, at the same temperature $T_0$ the vapor pressure of the solution ($P_1$) is lowered (due to the presence of the nonvolatile solute) compared to that of the pure solvent ($P_0$). Also, at a lower temperature $T_1$ the vapor pressure on the solution curve is $P_2$ (with $P_2 < P_1$). Thus, the order is $P_0 > P_1 > P_2$. Option B is correct.

3. Option C: The freezing point depression is derived using the Clausius–Clapeyron relation (applied to the fusion process). It leads to:

   $$\ln\Big(\frac{P_0}{P_2}\Big) = \frac{\Delta H_{fusion}}{R}\left(\frac{1}{T_1} - \frac{1}{T_0}\right)$$

   Rewriting $\frac{1}{T_1} - \frac{1}{T_0} = \frac{T_0-T_1}{T_0T_1}$ gives:

   $$P_0 = P_2 \exp\left[\frac{\Delta H_{fusion}}{R}\frac{T_0-T_1}{T_0T_1}\right]$$

   So, option C is correct.

4. Option D: Similarly, applying the Clausius–Clapeyron equation to the vaporization process for the solution,

   $$\ln\Big(\frac{P_1}{P_2}\Big) = \frac{\Delta H_{vap}}{R}\left(\frac{1}{T_1} - \frac{1}{T_0}\right)$$

   which rewrites to:

   $$P_1 = P_2 \exp\left[\frac{\Delta H_{vap}}{R}\frac{T_0-T_1}{T_0T_1}\right]$$

   Making option D also correct.