Question

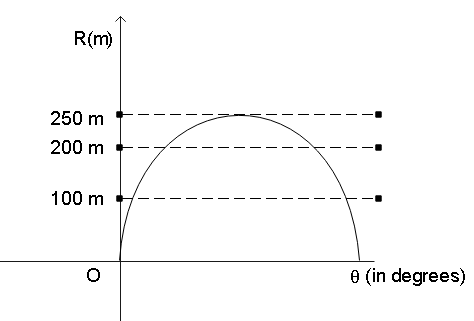
From the ground level, a ball is to be shot with a certain speed. Graph shows the range $R$ it will have versus the launch angle $\theta$ . The least speed the ball will have during its flight, if $\theta$ is chosen such that the flight time is half of its maximum possible value, is equal to (take $g{\text{ }} = {\text{ }}10{\text{ }}m/{s^2}$ )

A) $250\,\,m/s$
B) $50\sqrt 3 \,m/s$
C) $50\,m/s$
D) $25\sqrt 3 \,m/s$

Answer 1

Determine the launch angle given that flight time should be half of its maximum possible value. Use the graph to determine the launch velocity for the maximum range of a projectile. The least speed of an object during a projectile occurs at the topmost point in its trajectory where it’ll only have a horizontal component of velocity.

Formula used:
Flight time of projectile: $T = \dfrac{{2u\sin \theta }}{g}$ where $u$ is the launch velocity, $\theta$ is the launch angle and $g$ is the gravitational acceleration
Range of projectile: $R = \dfrac{{{u^2}\sin 2\theta }}{g}$

Complete step by step solution:
We’ve been given that the flight time should be half of its maximum values. Since, $\sin 90^\circ = 1$ , the maximum time flight will be
${T_{max}} = \dfrac{{2u}}{g}$
However for the time flight to be half of its maximum values, the launch angle will have to be $30^\circ$ since $\sin 30^\circ = \dfrac{1}{2}$ .
T = \dfrac{{2u \times \dfrac{1}{2}}}{g} \\\ = \dfrac{u}{g} \\\
From the graph, we notice that the maximum projectile range is given to be $250m$ which we know is obtained when the launch angle is $45^\circ$ .
Thus using the formula for the range of a projectile,
$R = \dfrac{{{u^2}\sin 2\theta }}{g}$ ,
We substitute $R = 250$ for $\theta = 45^\circ$ and obtain
$250 = \dfrac{{{u^2}\sin 90^\circ }}{{10}}$
On multiplying both sides by 10 and taking the square root, we get:
$u = 50m/s$
Now the minimum velocity of the projectile in flight happens when it is at its topmost point in the projectile since there is no vertical velocity component. The horizontal component of velocity at the topmost point corresponds to the least speed of the ball and can be calculated as
{v_{min}} = u\cos \theta \\\ = 50\cos (30^\circ ) \\\
Placing the value of $\cos 30^\circ = \sqrt 3 /2$ , we get:
${v_{min}} = 25\sqrt 3$ which corresponds to option (D).

Note:
In order to solve such questions, we must be aware about the phenomenon of projectile motion and some of its basic formulae. We’ve been provided with the values of launch angle and the launch speed indirectly which are needed to find the lowest speed of the projectile.