Question

From the following data, the activation energy for the reaction $(Cal/mol)$ is:
${{H}_{2}}+{{I}_{2}}\to 2HI$

A. $4\times {{10}^{4}}$
B. $2\times {{10}^{4}}$
C. $8\times {{10}^{4}}$
D. $3\times {{10}^{4}}$

Answer 1

To solve this question, look at the parameters given to us in the question. Both the terms i.e. the activation energy and temperature are related by Arrhenius equation. So, put the values given in the equation to obtain the required answer.

Complete step by step solution:
Let us first discuss the equation, there is an equation named as Arrhenius equation, that provides a dependence of rate of a chemical reaction on temperatures. Mathematically, it is represented as:
$k=A{{e}^{-\dfrac{{{E}_{a}}}{RT}}}$
Where, $k$ is the rate of the reaction,
$A$ is the Arrhenius constant or collision frequency or collision factor,
${{E}_{a}}$ is the activation energy,
$R$ is the universal gas constant which equals to $8.314J/mol-K$, and
$T$ is the temperature.
So, this equation can also be written as:
$\log k=\log A-\dfrac{{{E}_{a}}}{RT}$
Now, coming back to the question, we are given data where the temperature and rate of reaction are given and we know the value of universal gas constant.
So, given that:
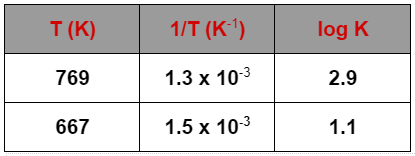
$\log {{K}_{1}}=2.9$,
$\log {{K}_{2}}=1.1$,
${{T}_{1}}=769$,
${{T}_{2}}=667$,
$\dfrac{1}{{{T}_{1}}}=1.3\times {{10}^{-3}}$, and
$\dfrac{1}{{{T}_{2}}}=1.5\times {{10}^{-3}}$.
So, placing these values in the above equation, we get:
$\log {{K}_{1}}=\log A-\dfrac{{{E}_{a}}}{R{{T}_{1}}}$
Then, $2.9=\log A-\dfrac{{{E}_{a}}}{2.303R\times 769}$ --(i)
Similarly, $\log {{K}_{2}}=\log A-\dfrac{{{E}_{a}}}{R{{T}_{2}}}$
Then, $1.1=\log A-\dfrac{{{E}_{a}}}{2.303R\times 667}$ --(ii)
Now, by subtracting equation (i) and equation (ii), we will get:
$1.8=\dfrac{{{E}_{a}}}{2.303R}\left[ \dfrac{1}{{{T}_{2}}}-\dfrac{1}{{{T}_{1}}} \right]$
So, now putting the value of the temperatures,
$1.8=\dfrac{{{E}_{a}}}{2.303R}\left[ 1.5\times {{10}^{-3}}-1.3\times {{10}^{-3}} \right]$
Then, $1.8=\dfrac{{{E}_{a}}}{2.303R}\times 0.2\times {{10}^{-3}}$
Then, ${{E}_{a}}=\dfrac{1.8\times 2.303\times 0.08314}{0.2\times {{10}^{-3}}}$
So, ${{E}_{a}}=4.17\times {{10}^{4}}Cal/mol$
Therefore, the activation energy for the above reaction is $4.17\times {{10}^{4}}Cal/mol\cong 4\times {{10}^{4}}Cal/mol$.

Hence, the correct option is A.

Note: While calculating, consider the units of each parameter given and you should have knowledge about the Arrhenius equation. The activation energy is always positive and it is referred to as the amount of energy required to bring out the reaction. In the real world, there is no reaction which has zero activation energy because when activation energy is zero, then there will be effective collisions between the particles.