Question

From the choices given below, choose the equation whose graphs are given in Figure (i) and Figure (ii).

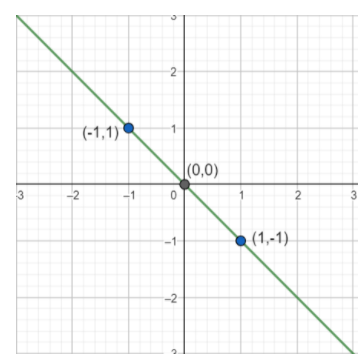
Figure(i)

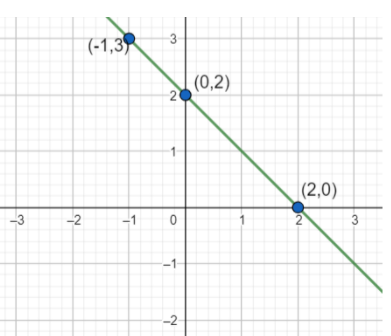
figure (ii)

Answer 1

Hint: For both the graphs, we are given three points each which line the required line and hence, will satisfy the equation of the line. So, using this fact, substitute all these points one by one in the given options. The option for which all the three points satisfy will be the final answer.

In this question, we are given two graphs.
We need to find the equations of these graphs from the choices provided to us.
Let us start by Figure (i).
In the given Figure (i), the solutions of the equation are (−1, 1), (0, 0) and (1, −1).
The equation which satisfies these solutions is the correct equation.
$x + y = 0$ satisfies these solutions.
Proof:
If we put the value of $x = −1$ and $y = 1$ in the equation $x + y = 0$
$x + y = −1 + 1 = 0$
L.H.S = R.H.S
If we put the value of $x = 0$ and $y = 0$
$x + y = 0 + 0 = 0$
L.H.S = R.H.S
If we put the value of $x = 1$ and $y = −1$
$x + y = 1 + (−1) = 1 – 1 = 0$
L.H.S = R.H.S
Hence, option (b) $x + y = 0$ is correct for figure (i).
Similarly, we will solve for figure (ii).
In the given Figure (ii) the solutions of the equation are (−1, 3), (0, 2) and (2, 0).
The equation which satisfies these solutions is the correct equation.
Equation $y = −x + 2$ satisfies these solutions.
Proof:
If we put the value of $x = −1$ and $y = 3$ in the equation $y = −x + 2$
$y = −x + 2$
$3 = −(−1) + 2$
$3 = 3$
L.H.S = R.H.S
If we put the value of $x = 0$ and $y = 2$
$y = −x + 2$
$2 = −0 + 2$
$2 = 2$
L.H.S = R.H.S
If we put the value of $x = 2$ and $y = 0$
$y = −x + 2$
$0 = −2 + 2$
$0 = 0$
L.H.S = R.H.S
Hence, option (c) $y = −x + 2$ is correct for figure (ii).

Note: We can solve this question using another method also. In both the figures, we are given three points which lie on the line. We know that the equation of a line using two points (a, b) and (c, d) is given by $y-b=\dfrac{b-d}{a-c}\left( x-a \right)$. Using this formula, you can find the equation of the graphs quickly and you will have to use only two points in each case.