Question

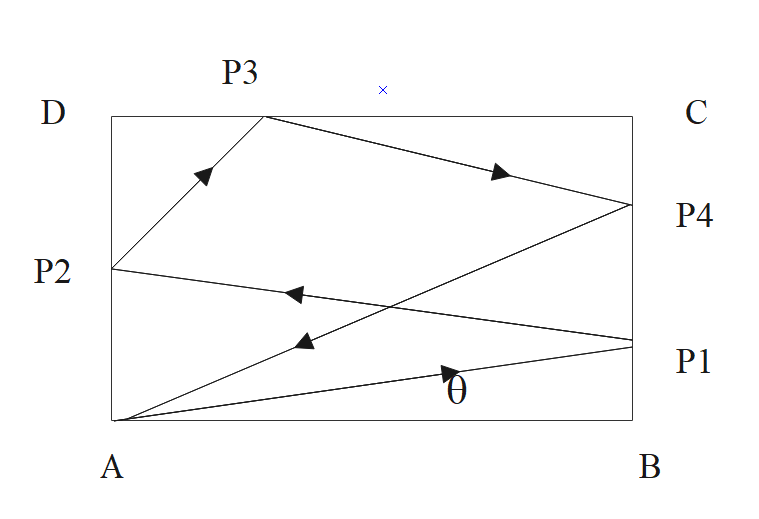
From one corner A of a rectangular billiard table ABCD placed on a horizontal surface, a ball of mass and negligible dimension is projected in the direction making θ with side AB it strikes in other sides BC, AD, DC and BC and then return to same point A. Then the value of coefficient of restitution is:

Answer 1

Find the time taken by the ball of negligible mass. Time taken is equal to the distance divided by the velocity of the negligible ball. Also, the velocity is also derived from the coefficient of restitution. Next, the vertical and horizontal equations are taken and solved together.

Complete answer:
Let us find the time taken by the negligible ball before every strike.
For the point $A{{P}_{1}}$, the time taken is equal to
${{t}_{1}}=\dfrac{a}{u\cos \theta }$
Also, the time taken can also be written as,
${{t}_{1}}=\dfrac{B{{P}_{1}}}{u\sin \theta }$
This is the time taken in the vertical component of velocity.
Similarly, the same will be written for all the strikes,
So, the time taken for the negligible mass to travel ${{P}_{1}}{{P}_{2}}$will be,
${{t}_{2}}=\dfrac{a}{eu\cos \theta }=\dfrac{{{P}_{2}}D}{u\sin \theta }$
The time taken by the negligible mass to travel ${{P}_{3}}{{P}_{4}}$will be,
${{t}_{3}}=\dfrac{D{{P}_{3}}}{{{e}^{2}}u\cos \theta }=\dfrac{{{P}_{2}}D}{u\sin \theta }$
The time taken by the negligible mass to travel ${{P}_{3}}{{P}_{4}}$
${{t}_{4}}=\dfrac{{{P}_{3}}C}{{{e}^{2}}u\cos \theta }=\dfrac{C{{P}_{4}}}{eu\sin \theta }$
The time taken by the negligible mass to travel ${{P}_{5}}A$
${{t}_{5}}=\dfrac{a}{{{e}^{3}}u\cos \theta }=\dfrac{{{P}_{4}}B}{eu\sin \theta }$
As the time taken is same if taken in vertical component or horizontal component,
The time taken when velocity is chosen in vertical component=time taken when velocity is chosen in horizontal component
$\begin{aligned} & \dfrac{a}{u\cos \theta }+\dfrac{a}{eu\cos \theta }+\dfrac{D{{P}_{3}}}{{{e}^{2}}u\cos \theta }+\dfrac{{{P}_{3}}C}{{{e}^{2}}u\cos \theta }+\dfrac{a}{{{e}^{3}}u\cos \theta }=\dfrac{{{P}_{4}}B}{eu\sin \theta }+\dfrac{C{{P}_{4}}}{eu\sin \theta }+\dfrac{{{P}_{2}}D}{u\sin \theta }+\dfrac{{{P}_{2}}D}{u\sin \theta }+\dfrac{B{{P}_{1}}}{u\sin \theta } \\\ & \Rightarrow \dfrac{a}{\cos \theta }(1+\dfrac{1}{e}+\dfrac{1}{{{e}^{2}}}+\dfrac{1}{{{e}^{3}}})=\dfrac{b}{\sin \theta }(1+\dfrac{1}{e}) \\\ & \Rightarrow e=\sqrt{\dfrac{a\sin \theta }{b\cos \theta -a\sin \theta }} \\\ \end{aligned}$

Additional Information:
The coefficient of restitution (COR) also denoted by (e) is the ratio of the final to initial relative velocity between two objects after they collide. It normally ranges from 0 to 1 where 1 would be a perfectly elastic collision. If the coefficient is high (very close to 1.00) it means that very little kinetic energy was lost during the collision. If the coefficient is low (close to zero) it suggests that a large fraction of the kinetic energy was converted into heat or was otherwise absorbed through deformation. Let's take a closer look.When a moving object (say a rubber ball) collides with an immobile flat surface (say a massive marble floor), the object will rebound with some fraction of its original energy. If the collision is perfectly elastic, then the ball will rebound with all of the energy it arrived with and its rebound velocity will be the same as its approach velocity. In this case, the coefficient of restitution is said to be precisely 1.00. On the other hand, if there is considerable permanent deformation of either the object or the surface (or both) then the object will rebound with much less energy than it originally arrived with. In this case, the coefficient of restitution will be close to zero.

Note:
The coefficient of restitution depends to a large extent on the nature of the two materials of which the colliding objects are made. It is also affected by the impact velocity, the shape and size of the colliding objects, the location on the colliding objects at which the collision occurs, and their temperatures.