Question

From any point P on the parabola ${{y}^{2}}=4ax$, a perpendicular PN is drawn on the axis meeting at N, the normal at P meets the axis in G. Prove that the sub-normal NG is equal to its semi-latus rectum.

Answer 1

Hint: First of all, draw the figure according to the information given in the question. Now, take the point $P\left( {{x}_{1}},{{y}_{1}} \right)$ and write the equation of normal at P and from that find the x coordinate of point G which is the point at which normal meets the x axis and take N as a point at which perpendicular from P meets x axis. Now, subtract ON from OG to find NG.

Complete step-by-step answer:
Here, we are given that from any point P on the parabola ${{y}^{2}}=4ax$, a perpendicular PN is drawn on the axis meeting at N, the normal at P meets the axis in G. We have to prove that the sub-normal NG is equal to its semi-latus rectum.

In the above figure, P is a point on the parabola from which a perpendicular is drawn on the axis of parabola meeting it at N. Also, the normal at point P is meeting the axis at G. Now, let us find the length of the sub-normal NG. Let the coordinates of the point P on parabola be $\left( {{x}_{1}},{{y}_{1}} \right)$. We are given that PG is normal at point P. So, let us write the equation of normal of the parabola ${{y}^{2}}=4ax$.
We know that equation of any line at $\left( {{x}_{1}},{{y}_{1}} \right)$ and slope m is given by, $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$. Let the slope of the normal be ${{m}_{N}}$. So, we get the equation of normal of parabola at point $P\left( {{x}_{1}},{{y}_{1}} \right)$ as, $\left( y-{{y}_{1}} \right)={{m}_{N}}\left( x-{{x}_{1}} \right).........\left( i \right)$
We know that slope of tangent of parabola at $\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $\dfrac{2a}{{{y}_{1}}}$. We also know that,
(slope of tangent) $\times$ (slope of normal) = -1. So, we get,
$\begin{aligned} & \left( \dfrac{2a}{{{y}_{1}}} \right)\times \left( {{m}_{N}} \right)=-1 \\\ & {{m}_{N}}=\dfrac{-{{y}_{1}}}{2a} \\\ \end{aligned}$
By substituting the value of ${{m}_{N}}$ in equation (i), we get,
$\left( y-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2a}\left( x-{{x}_{1}} \right)$
$2ay-2a{{y}_{1}}=-{{y}_{1}}x+{{y}_{1}}{{x}_{1}}$
So, we get the equation of normal PG as,
$2ay=2a{{y}_{1}}+{{y}_{1}}{{x}_{1}}-{{y}_{1}}x.........\left( ii \right)$
Now we know that G lies on x axis, so y coordinate of G would be 0. So, by substituting y = 0 in equation (ii), we will get,
$\begin{aligned} & 0=2a{{y}_{1}}+{{y}_{1}}{{x}_{1}}-{{y}_{1}}x \\\ & 0=\left( 2a+{{x}_{1}}-x \right){{y}_{1}} \\\ & 2a+{{x}_{1}}-x=0 \\\ & x=2a+{{x}_{1}} \\\ \end{aligned}$
So, we get the coordinate of G as $\left( 2a+{{x}_{1}},0 \right)$. Now, we are given that ON is perpendicular to NP. So, x coordinate of N and P would be the same. We get the coordinate of N as $\left( {{x}_{1}},0 \right)$. Now, since the x coordinate of N is ${{x}_{1}}$. So, we get $ON={{x}_{1}}$. Also, x coordinate of G is $2a+{{x}_{1}}$. So, we get $OG=2a+{{x}_{1}}$

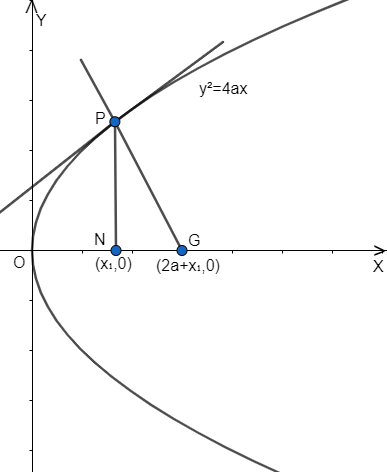
Now, from the figure, we can see that NG = OG – ON. So, we get $NG=\left( 2a+{{x}_{1}} \right)-\left( {{x}_{1}} \right)$. Length of subnormal, $NG=2a.........\left( iii \right)$
Now, we know that for any parabola ${{y}^{2}}=4ax$, the length of latus rectum = 4a. So, we get the length of the semi-latus rectum as,
$\begin{aligned} & \dfrac{4a}{2} \\\ & =2a.........\left( iv \right) \\\ \end{aligned}$
From equation (iii) and equation (iv), we get,
Length of subnormal NG = Length of the semi-latus rectum
Hence proved.

Note: In this question, students must first draw the figure to clearly visualize the question. Also, students can directly remember that the length of subnormal is constant for parabola and is equal to half of the latus rectum. So, that they won’t need to do the calculations each time while solving questions related to the sub-normal. Also, students are advised to remember the equations of tangent and the normal of parabola which are $y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)$ and $\left( y-{{y}_{1}} \right)=\dfrac{-{{y}_{1}}}{2a}\left( x-{{x}_{1}} \right)$ respectively.