Question

From an external point P, a tangent PT and a line segment PAB are drawn to a circle with centre O. Prove that $PA.PB={{\left( PT \right)}^{2}}$

Answer 1

To solve the question, we have to draw a perpendicular from the centre of the circle to line segment AB to get equations of PA, PB. To solve further, apply right-angle triangle symmetry rule which states two right-angle triangles are congruent when hypotenuse is equal along with common angle. To calculate the answer, apply Pythagorean theorem to ease the procedure of solving.

Complete step-by-step answer :

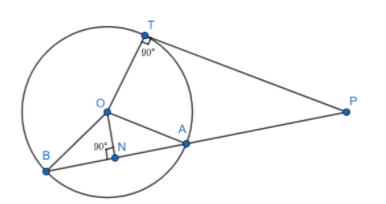
Draw a perpendicular to AB from the centre of triangle O to a point N.
Thus, ON is perpendicular to AB.
From the above diagram we get,
PN = PA + AN
Thus, the length of PA can also be written as PN - AN.
PA = PN – AN …. (1)
From the above diagram we get,
PB = PN + BN …. (2)
Thus, the length of PB can also be written as PN + BN.
By multiplying of equations (1) and (2), we get
PA. PB = (PN – AN). (PN + BN) ……(3)
Consider $\Delta ONA$ and $\Delta ONB$
We know OA = OB since OA and OB are equal to radius of the circle.
We know $\angle ONA=\angle ONB$ since the value of $\angle ONA,\angle ONB$ is equal to ${{90}^{0}}$ since ON is perpendicular to AB.
Thus, $\Delta ONA$ and $\Delta ONB$ are congruent by hypotenuse and right-angle symmetry of the right-angle triangle.
We know that in congruent triangles their corresponding sides are equal.
Thus, we get,
AN = BN
By substituting the above value in equation (3), we get
PA. PB = (PN – AN). (PN + AN)
$PA.\text{ }PB\text{ }=\text{ P}{{\text{N}}^{2}}-A{{N}^{2}}$ ….. (4)
Since we know the formula $\left( a+b \right)\left( a-b \right)=\text{ }{{a}^{2}}-{{b}^{2}}$
We know that by Pythagorean theorem, we get, in a right-angle triangle XYZ $X{{Z}^{2}}=\text{ X}{{\text{Y}}^{2}}+Y{{Z}^{2}}$ where XZ is hypotenuse and XY, YZ are two adjacent sides of the given right-angle triangle.
By applying the above theorem for $\Delta ONP$ and $\Delta ONA$ , both right angled at N, we get we get
$O{{P}^{2}}=\text{ O}{{\text{N}}^{2}}+P{{N}^{2}}$
$O{{A}^{2}}=\text{ O}{{\text{N}}^{2}}+A{{N}^{2}}$
By subtracting the above two equations, we get
$O{{P}^{2}}-O{{A}^{2}}=\text{ P}{{\text{N}}^{2}}-A{{N}^{2}}$
$\text{P}{{\text{N}}^{2}}-A{{N}^{2}}=O{{P}^{2}}-O{{A}^{2}}$ …… (5)
We know OA = OB = OT since OA, OB, OT are equal to radius of the circle.
By substituting the above value in the equation (5), we get
$\text{P}{{\text{N}}^{2}}-A{{N}^{2}}=O{{P}^{2}}-O{{T}^{2}}$
By applying Pythagorean theorem for $\Delta POT$, right-angled at T, we get
$O{{P}^{2}}=\text{P}{{\text{T}}^{2}}+O{{T}^{2}}$
$\text{P}{{\text{T}}^{2}}=O{{P}^{2}}-O{{T}^{2}}$
Thus, by substituting equation (5) in the above equation, we get
$\text{P}{{\text{N}}^{2}}-A{{N}^{2}}=P{{T}^{2}}$
Thus, by substituting equation (4) in the above equation, we get
$PA.PB={{\left( PT \right)}^{2}}$
Thus, we get $PA.PB={{\left( PT \right)}^{2}}$
Hence, proved.

Note :The possibility of mistake can be not drawing perpendicular from the centre of the circle to AB, which eases the procedure of solving. The other possibility of mistake can be not applying triangle symmetry rule and Pythagorean theorem to do further calculation.