Question

From an aeroplane vertically above a straight horizontal road , the angles of depression of two consecutive kilometres stones on (i) opposite (ii) same sides of aeroplane are observed to be $30^\circ$ and $60^\circ$ . Find the height of the aeroplane above the road in two cases .

Answer 1

As we have to find the vertical height of the aeroplane in case (i) Consider the both stone is opposite to the aeroplane and the distance between them is a kilometre in the case (ii) Consider the both stone at the same side of the aeroplane and the distance between them is a kilometre now solve both the cases by using the $\tan \theta = \dfrac{{{\text{Altitude}}}}{{{\text{Base}}}}$ .

Complete step-by-step answer:
In this question it is given that the an aeroplane vertically above a straight horizontal road , the angles of depression of two consecutive kilometres stones so for the opposite side
the figure become

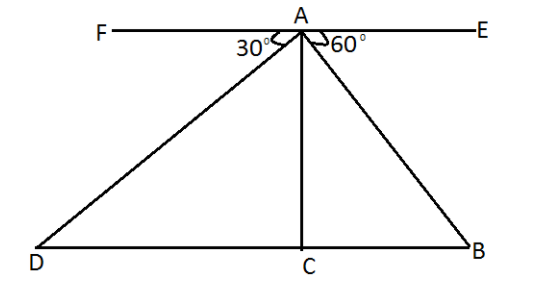
Where at point A the aeroplane is it , and angle of depression is given in the figure as in the question the distance between the stones is $1$ km hence DB = $1$ km
Let the vertical height AC is $x$ km and DC = $y$
As from the Transverse angle $\angle {\text{ADC = 30}}^\circ$ and $\angle {\text{ABC = 60}}^\circ$

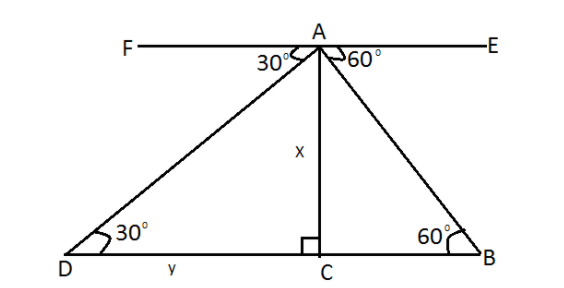
In triangle ADC , AC is perpendicular to DB therefore ,
$\tan 30^\circ = \dfrac{{{\text{AC}}}}{{{\text{DC}}}}$ = $\dfrac{x}{y}$
As we know that the $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ on putting the above
$\Rightarrow$ $\dfrac{1}{{\sqrt 3 }} = \dfrac{x}{y}$
$y = \sqrt 3 x$ .........(i)
In triangle ABC , AC is perpendicular to DB therefore
$\tan 60^\circ = \dfrac{{{\text{AC}}}}{{{\text{BC}}}}$
As it is given that DB is $1$ km and DC = $y$ hence BC = $1 - y$
$\Rightarrow$ $\tan 60^\circ = \dfrac{x}{{1 - y}}$
As from equation (i) $y = \sqrt 3 x$ and we know that $\tan 60^\circ = \sqrt 3$ , On putting it in above equation
$\Rightarrow$ $\sqrt 3 = \dfrac{x}{{1 - \sqrt 3 x}}$
On cross multiplication ,
$\Rightarrow$ $\sqrt 3 - 3x = x$
$\Rightarrow$ $4x = \sqrt 3$
Hence $x = \dfrac{{\sqrt 3 }}{4} = 0.433$
Hence the vertical distance in opposite case is $0.433$ Km
(ii) If the stones are at the same side the

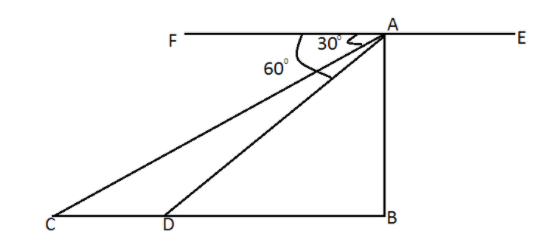
Where at point A the aeroplane is it , and angle of depression is given in the figure as in the question the distance between the stones is $1$ km hence DC = $1$ km
Let the vertical height AB is $x$ km and DB = $y$
As from the Transverse angle $\angle {\text{ACB = 30}}^\circ$ and $\angle {\text{ADB = 60}}^\circ$

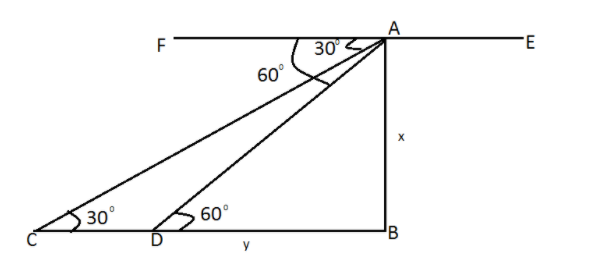
In triangle ADB , AB is perpendicular to DB therefore ,
$\tan 60^\circ = \dfrac{{{\text{AB}}}}{{{\text{DB}}}}$ = $\dfrac{x}{y}$
As we know that the $\tan 60^\circ = \sqrt 3$ on putting the above
$\Rightarrow$ $\sqrt 3 = \dfrac{x}{y}$
$\Rightarrow$ $y = \dfrac{x}{{\sqrt 3 }}$ .........(i)
In triangle ABC , AB is perpendicular to DB therefore
$\tan 30^\circ = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}$
As it is given that DC is $1$ km and DB = $y$ hence BC = $1 + y$
$\Rightarrow$ $\tan 30^\circ = \dfrac{x}{{1 + y}}$
$\Rightarrow$ $\sqrt 3 + x = 3x$
As from equation (i) $y = \dfrac{x}{{\sqrt 3 }}$ and we know that $\tan 30^\circ =$\Rightarrow$\dfrac{1}{{\sqrt 3 }}$ , On putting it in above equation
$\Rightarrow$ $\dfrac{1}{{\sqrt 3 }} = \dfrac{x}{{1 + \dfrac{x}{{\sqrt 3 }}}}$
On cross multiplication , we get $2x = \sqrt 3$
$\Rightarrow$ $1 + \dfrac{x}{{\sqrt 3 }} = \sqrt 3 x$
Taking LCM on LHS then cross multiple ,
$\Rightarrow$ $\dfrac{{\sqrt 3 + x}}{{\sqrt 3 }} = \sqrt 3 x$
On solving further ,
$\Rightarrow$ $x = \dfrac{{\sqrt 3 }}{2} = 0.866$
Hence the vertical distance in opposite case is $0.866$ Km

Note: The angle of elevation is defined as an angle between the horizontal plane and oblique line from the observer’s eye to some object above his eye.
The angle of depression is defined as an angle constructed by a horizontal line and the line joining the object and observer’s eye