Question

From an aeroplane flying vertically above a two horizontal road, the angle of depression of two consecutive stones on the same side of the aeroplane are observed to be ${30^ \circ }$ and ${60^ \circ }$ respectively. The height at which the aeroplane is flying (in km) is
A. $\dfrac{4}{{\sqrt 3 }}$
B. $\dfrac{{\sqrt 3 }}{2}$
C. $\dfrac{2}{{\sqrt 3 }}$
D. $2$

Answer 1

Hint : We have been given that we have two consecutive stones, so we will use the fact that the distance between two consecutive stones is one.
First we will assume that the distance of two consecutive stones be
$x,x + 1$ .
Now we have been given the angles of two stones, so we will now use the tan ratio for both the angles.
We know that
$\tan \theta = \dfrac{p}{b}$ , where
$p$ is the perpendicular and
$b$ is the base of the triangle.

Complete step-by-step answer :
Let us assume that the distance of two consecutive stones be
$x,x + 1$ .
Now we will draw the diagram according to the data given in the question:

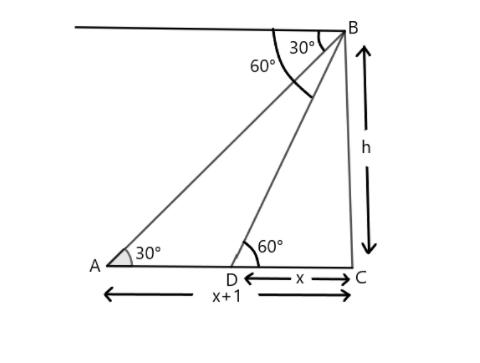
We have to find the height at which aeroplane is flying i.e.
$BC$ .
We will now take the triangle, In triangle BCD, we have Perpendicular
$BC = h$ and the base is
$DC = x$ .
We know the formula
$\tan \theta = \dfrac{p}{b}$ .
In this triangle a angle i.e.
$\theta = {60^ \circ }$ .
And we know that the value of $\tan 60^\circ$ is
$\sqrt 3$ .
Now by substituting the values in the formula we can write
Or,
$\sqrt 3 = \dfrac{h}{x}$ .
By cross multiplication, it gives
$\sqrt 3 x = h \Rightarrow x = \dfrac{h}{{\sqrt 3 }}$ .
Now in another triangle i.e. In $\Delta ABC$ ,
We know the value i.e.
$\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ ,
So we can write
$\tan 30^\circ = \dfrac{h}{{x + 1}}$ ,
By putting the value, we have
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + 1}}$ .
By cross multiplication, we can write
$x + 1 = \sqrt 3 h$
From the above we can substitute the value of $x$ by
$x = \dfrac{h}{{\sqrt 3 }}$
So it gives:
$\dfrac{h}{{\sqrt 3 }} + 1 = \sqrt 3 h$
We can group the similar terms together:
$\sqrt 3 h - \dfrac{h}{{\sqrt 3 }} = 1$
By taking the LCM in the left hand side we have:
$\dfrac{{\sqrt 3 \times \sqrt 3 h - h}}{{\sqrt 3 }} = 1 \Rightarrow \dfrac{{3h - h}}{{\sqrt 3 }} = 1$
On simplifying the value, it gives
$\dfrac{{2h}}{{\sqrt 3 }} = 1$
Or, by cross multiplying it can be written as
$h = \dfrac{{\sqrt 3 }}{2}$
Hence the correct option is (B) $\dfrac{{\sqrt 3 }}{2}$ .
So, the correct answer is “Option B”.

Note : We should note that in $\Delta ABC$ , we have perpendicular is the same i.e.
$BC = h$ and the base is the total length of AC i.e.
$AC = x + 1$ .
And the angle given is $30^\circ$ , so we put the value of
$\tan 30^\circ = \dfrac{{BC}}{{AC}}$
Or,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + 1}}$ .
Note here we have to find the value of ‘h’ so we modify both equations in terms of h.