Question

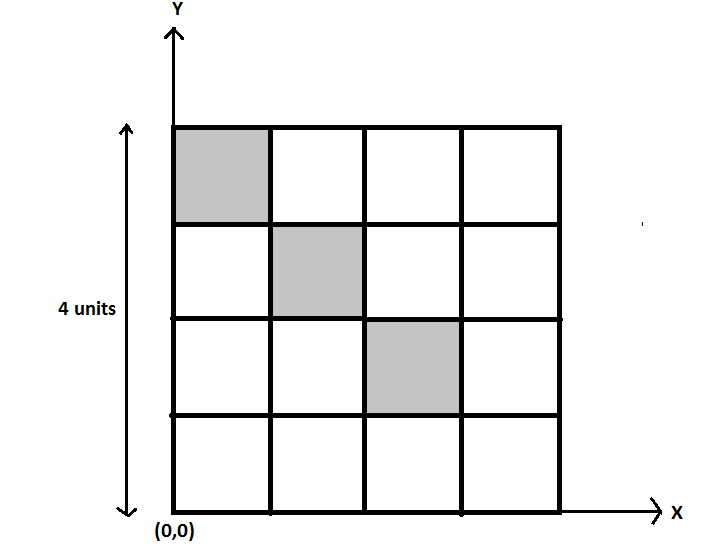
From a uniform square plate, the shaded portion was removed as shown in the figure. Find the coordinates of the center of mass of the remaining plate. X-Y axes and origin are shown in the figure.

Answer 1

In this question, it is given that the square plate is uniform which implies that the mass is distributed evenly throughout the plate. We have to find the center of mass of the whole plate and subtract the center of mass of the shaded plates to get the coordinates of the remaining plate. As the plate is uniform, the center of mass will lie on the centroid of the body. Hence we have to find the coordinates of the center of mass of the shaded portion with the help of a diagram.

Complete step by step answer:
We know that the side of the square is 4 units. Now, we know that the center of mass of the plate as a whole i.e. without missing parts would be $\left( {\dfrac{4}{2},\dfrac{4}{2}} \right) = (2,2)$ due to symmetry as shown in the figure given below.

As the square is divided into 16 small parts therefore the length of a side of one small square will be 1 unit as shown. Now, we have to find the center of mass of the shaded portion of the plate using the coordinates in the figure. The center of mass of a given rigid body with two particles is given as:
${X_{com}} = \dfrac{{{m_1}{r_1} + {m_2}{r_2}}}{{{m_1} + {m_2}}}$
Where,
${X_{com}}$ is the center of mass coordinate.
${m_{1\,}},\,{m_2}$ are the masses of the two-particles.
${r_{1\,\,}},{r_2}$ are the distance of the particle from the origin as a reference.
We will now consider the shaded plate in the first row and first column. As the plate is uniform, the center of mass of this portion of the plate will lie at its center having coordinates $(0.5,3.5)$ as shown in the figure. Here we used symmetry and coordinate geometry. Similarly, for the shaded portion in the second row and second column, its center of mass would lie at $(1.5,2.5)$ and for the shaded portion in the third row and third column, the center of mass would lie at $\left( {2.5,1.5} \right)$ .
Now let us assume, the mass of the square plate be ‘$M$’ and the mass of each small plate be ‘$m$’.
We know that the area of the square is the square of its side. So,
Area of the big square, $A = 4\,unit \times 4\,unit = 16\,uni{t^2}$
Area of a small plate, $a = 1\,unit \times 1\,unit = 1\,uni{t^2}$
But the areal density of both the small square plates and the big square plate is equal as the plate is uniform. We know that,
Areal density, $D = \dfrac{{Mass}}{{Area}}$
The areal density of bigger plate, $D = \dfrac{M}{A}$
The areal density of smaller plate, $D = \dfrac{m}{a}$
Equating the areal density of both plates and putting the value of area we get,
$\dfrac{M}{A} = \dfrac{m}{a}$
$\Rightarrow \dfrac{M}{{16}} = \dfrac{m}{1}$
$\Rightarrow \,m = \dfrac{M}{{16}}......(1)$
We have to find the center of the mass coordinate of the remaining plate. For this, we have to subtract the center of mass of the shaded portions from the big square plate.
Three shaded plates together have mass $3m$ and the x coordinates are taken with origin as a reference from the figure, we get,
${X_{com}} = \dfrac{{M(2) - m(0.5) - m(1.5) - m(2.5)}}{{M - 3m}}.....(2)$
Putting the value of $m$ from equation (1) into equation (2) we get,
${X_{com}} = \dfrac{{M(2) - \dfrac{M}{{16}}(0.5) - \dfrac{M}{{16}}(1.5) - \dfrac{M}{{16}}(2.5)}}{{M - 3\left( {\dfrac{M}{{16}}} \right)}}\,$
Taking the LCM of the denominator and solving further we get,
${X_{com}} = \dfrac{{\left( {\dfrac{{32M - 4.5M}}{{16}}} \right)}}{{\left( {\dfrac{{16M - 3M}}{{16}}} \right)}}$
$\Rightarrow {X_{com}} = \dfrac{{27.5M}}{{13M}}$
$\Rightarrow {X_{com}} = 2.11\,unit$
Similarly, the y coordinates are taken with origin as a reference from the figure, we get,
${Y_{com}} = \dfrac{{M(2) - m(3.5) - m(2.5) - m(1.5)}}{{M - 3m}}\,......(3)$
Putting the value of $m$ from equation (1) into equation (3) we get,
${Y_{com}} = \dfrac{{M(2) - \dfrac{M}{{16}}(3.5) - \dfrac{M}{{16}}(2.5) - \dfrac{M}{{16}}(1.5)}}{{M - 3\left( {\dfrac{M}{{16}}} \right)}}\,$
Taking the LCM of the denominator and solving further we get,
${Y_{com}} = \dfrac{{\left( {\dfrac{{32M - 7.5M}}{{16}}} \right)}}{{\left( {\dfrac{{16M - 3M}}{{16}}} \right)}}$
$\Rightarrow {Y_{com}} = \dfrac{{24.5M}}{{13M}}$
$\Rightarrow {Y_{com}} = 1.88\,unit$
So, the coordinates of the remaining plate are $(2.11,1.88)$ .

Note: The center of mass is a point where if force is applied, it moves in its direction without any angular acceleration. For a single rigid body, the center of mass is fixed and if the body is uniform i.e. its density is the same everywhere then the center of mass lies at the centroid of the body. This concept is used in aeronautical engineering to design helicopters and airplanes. Also, it is used in astronomy and astrophysics to find the center of mass of celestial bodies.