Question
Question: From a uniform square plate of side \[a\] and mass m, a square portion DEFG of side \[\dfrac{a}{2}\]...
From a uniform square plate of side a and mass m, a square portion DEFG of side 2a is removed. Then, the moment of inertia of remaining portion about the axis AB is
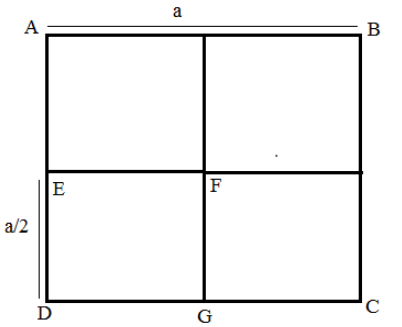
A. 167ma2
B. 163ma2
C. 43ma2
D. 169ma2
Solution
To find out the moment of inertia of the part excluding DEFG part, we need to find the moment of inertia of the full square plate and subtract the moment of inertia of square DEFG about AB axis. Moreover, moment of inertia is defined as the quantity expressed by the body resisting angular acceleration which is the sum of the product of the mass of every particle with its square of a distance from the axis of rotation.
Complete step by step answer:
The formula for moment of inertia of square plate about a parallel axis through its centre of mass is 12ml2 where l the length of the side of the square is and m is the mass of the square plate.
First, we find the moment of inertia of the whole square about the axis AB. From parallel axis theorem, we have moment of inertia about a parallel axis through its centre of mass I=Io+md2, where Io is the moment of inertia about an axis through the centre of mass of the body, d is the distance between the axes, m is the mass of the body.
Moment of inertia of a square about an axis parallel to two of its sides and passing through the centre of mass is given by; I=12ml2, where m is the mass of the square and l is the length of the side.
Using parallel axis theorem, moment of inertia of the full square plate about the axis AB is
IABCD=12ma2+m(2a)2, where 12ma2 is the moment of inertia about the axis EI passing through the centre of mass and 2a is the distance between axis AB and EI
⇒IABCD=3ma2...................(i)
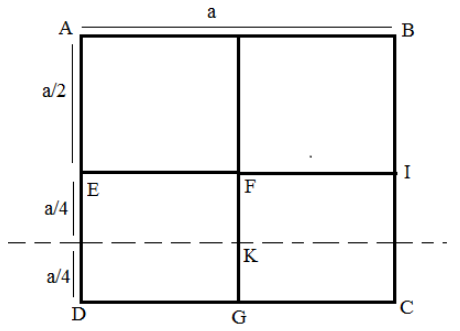
Now, we find out the moment of inertia of the square DEFG about the axis AB. Total mass ism, the mass of the square DEFG is 4m and the side is 2a. For the square DEFG the axis JK passes through its centre of mass. So, moment of inertia about JK for the square DEFG is
IJK=12(4m)(2a)2
The moment of inertia of square DEFG about the axis AB, using parallel axis theorem is
IDEFG=IJK+4m(2a+4a)2, where (2a+4a)is the distance between axis JK and AB.
⇒IDEFG=19228ma2...................(ii)
Now, when the square DEFG is removed, the moment of inertia of the remaining portion about axis AB is given by
Iremaining=IABCD−IDEFG
⇒Iremaining=3ma2−19228ma2
(Using values of IABCD and IDEFG from equations (i)and(ii))
∴Iremaining=163ma2
Therefore, the moment of inertia of the remaining portion is 163ma2. Hence, option B is correct.
Note: In case of moment of inertia, whenever some part of the body is removed or a part is added then we can apply the principle of superposition. But we should check that we are taking the moment of inertia about the same axis for all the parts. When a part is removed we can subtract the moment of inertia of that part from the moment of inertia of the full body as we have done in this question.
