Question

From a uniform disk of radius ${\text{R}}$, a circular hole of radius $\dfrac{{\text{R}}}{2}$ is cut out. The centre of the hole is at $\dfrac{{\text{R}}}{2}$ from the centre of the original disc. Locate the centre of gravity of the resulting flat body.

Answer 1

Hint: Assume that the mass per unit area of the uniform disc is $\sigma$ therefore the mass of the uniform disc is ${\text{M = }}\sigma \pi {{\text{R}}^2}$ and the mass of the small disc is $\sigma \pi {\left( {\dfrac{{\text{R}}}{2}} \right)^2} = \dfrac{{\sigma \pi {{\text{R}}^2}}}{4} = \dfrac{{\text{M}}}{4}$
Formula used:
${\text{x = }}\dfrac{{\left( {{{\text{m}}_1}{{\text{r}}_1}{\text{ + }}{{\text{m}}_2}{{\text{r}}_2}} \right)}}{{\left( {{{\text{m}}_1}{\text{ + }}{{\text{m}}_2}} \right)}}$
where ${\text{x}}$ is the distance through which the centre of gravity of the remaining portion shifts
and ${{\text{m}}_1},{{\text{r}}_1}$ are the mass & radius of uniform disc and ${{\text{m}}_2},{{\text{r}}_2}$ are the mass & radius of the small disc that has been cut.

Complete step-by-step solution -
__
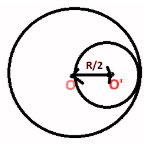
Given that,
Radius of uniform disc $= {\text{R}}$
Radius of the smaller disc $= \dfrac{{\text{R}}}{2}$
Let the mass per unit area of the original disc $= \sigma$
Therefore mass of the uniform disc $= {\text{M = }}\sigma \pi {{\text{R}}^2}$
And the mass of the small disc ${\text{ = }}\sigma \pi {\left( {\dfrac{{\text{R}}}{2}} \right)^2} = \dfrac{{\sigma \pi {{\text{R}}^2}}}{4} = \dfrac{{\text{M}}}{4}$
Now as the small disc has been cut from the uniform disc, the remaining portion is considered to be a system of two masses.
The two masses are: ${\text{M}}$ (concentrated at O) & $- {\text{M}}$(concentrated at O')
(negative sign indicating above that the portion is removed from the uniform disc)
Let ${\text{x}}$ be the distance through which the centre of mass of the remaining portion shifts from point O.
The relation between the centre of masses of two masses is give as:
${\text{x = }}\dfrac{{\left( {{{\text{m}}_1}{{\text{r}}_1}{\text{ + }}{{\text{m}}_2}{{\text{r}}_2}} \right)}}{{\left( {{{\text{m}}_1}{\text{ + }}{{\text{m}}_2}} \right)}} \\\ {\text{x = }}\dfrac{{\left[ {\left( {{\text{M}} \times {\text{0 - }}\dfrac{{\text{M}}}{4}} \right) \times \left( {\dfrac{{\text{R}}}{2}} \right)} \right]}}{{\left( {{\text{M - }}\dfrac{{\text{M}}}{4}} \right)}} \\\ = \dfrac{{\left( {\dfrac{{ - {\text{MR}}}}{8}} \right)}}{{\left( {\dfrac{{3{\text{M}}}}{4}} \right)}} \\\ = \dfrac{{ - 4{\text{R}}}}{{24}} \\\ {\text{x = }}\dfrac{{ - {\text{R}}}}{6} \\\$.

Note: The relation between the centre of masses of two masses is calculated by the formula ${\text{x = }}\dfrac{{\left( {{{\text{m}}_1}{{\text{r}}_1}{\text{ + }}{{\text{m}}_2}{{\text{r}}_2}} \right)}}{{\left( {{{\text{m}}_1}{\text{ + }}{{\text{m}}_2}} \right)}}$ which is found to be $\dfrac{{ - {\text{R}}}}{6}$ here the negative sign indicates that the centre of gravity of the resulting flat body gets shifted towards the left point O.