Question
Question: From a semi-circular disc of mass M and radius\({{R}_{2}}\). A semi-circular disc of radius \({{R}_{...
From a semi-circular disc of mass M and radiusR2. A semi-circular disc of radius R1 is removed as shown in the figure. If the mass of the original uncut disc is M. Find the momentum of inertia of the residual disc about an axis passing through centre O and perpendicular to the plane of the disc.
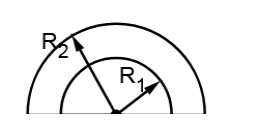
Solution
Hint: The moment of inertia of a point object about any axis is equal to the product of its mass and the square of the perpendicular distance between object and axis. To calculate the moment of inertia of any continuous mass system we break down the object into point mass and add moment of inertia of all point masses to get the moment of inertia of the entire system. We can also break the continuous mass system into a system of already known moment of inertia (for e.g. breaking discs into rings, etc.).
Complete step by step answer:
To calculate the moment of inertia of the remaining disc we will divide the disc into thin semicircular rings. In order to do so we will go to distance r (from centre O) and further by dr(where dr→0 ) take entire semicircular ring between r and dr
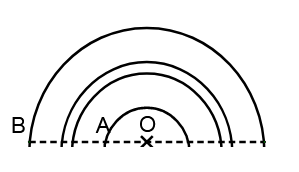
Now, our aim will be to first calculate the moment of inertia of this semicircular ring. We can clearly observe that every point of this semicircular ring is situated at equal distance from the axis, which is equal to the radius of the semicircular ring which is equal to r. So to calculate the moment of inertia of this semicircular ring we can simply multiply its mass to square of its radius. Since the disc has uniform mass distribution, we can get mass of a semicircular ring by multiplying its mass by surface mass density (i.e. mass per unit area).
Surface mass density of the disc will be its total mass divided by its total area i.e. πR222M. To calculate the area of a semicircular ring we can assume the semicircular ring is taken out from the disc and spread out. So now the semicircular ring will convert into a rectangle with length equal to its perimeter i.e. πr and breadth will be the width of the semicircular ring i.e. dr. So the area of the semicircular ring becomes a product of length and breadth which is πrdr .
Now moment of inertia of semicircular ring will be product its mass and square of its radius i.e.
R222Mrdr×r2=R222Mr3dr
This is the moment of inertia of a semicircular ring at distance r, now to calculate moment of inertia of complete disc we will add all such small semicircular rings covering the entire remaining disc. This can be achieved by integration and to cover the entire disc limit of r should be from R1 toR2.
So moment of inertia of remaining disc is
R1∫R2R222Mr3dr=R222MR1∫R2r3dr
On integration we will get
2R22M(R24−R14)
Hence the correct option is A.
Note: dr here is taken to be tending to zero so that we can assume the taken portion to be a ring. Often students make a mistake while calculating the value of surface mass density, while measuring it we should check that given mass is of original disc or mass of disc after being cut and accordingly divide it with area.
