Question

From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle . Prove that OT is the right bisector of line segment PQ.

Answer 1

Start by drawing the diagram and take triangles OPT and OQT , check for congruency and similarly triangles PRT and QRT , and apply CPCT for both of these congruent triangles . Take the sum of angle PRT and QRT as 180 and solve using the relation found.

Complete step-by-step answer :

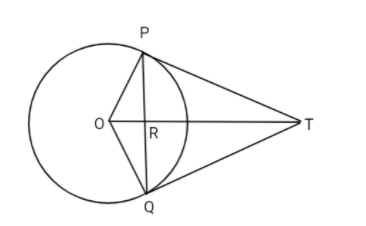
In the above diagram TP and TQ are tangents drawn from an external point to the circle. O is the centre of the circle.
Consider OT intersecting PQ at point R.
Now,
In$\vartriangle {\text{OPT and }}\vartriangle {\text{OQT}}$
OT = OT (common side)
TP = TQ (Tangents drawn from an external point to a circle are equal in length)
OP = OQ (Radius of the circle)
$\therefore \vartriangle {\text{OPT }} \cong {\text{ }}\vartriangle {\text{OQT}}$(by SSS congruency)
[SSS Postulate states that if two triangles have all the corresponding sides equal in length they are said to be congruent.]
By applying CPCT (Corresponding parts of congruent triangles)
$\angle {\text{OTP = }}\angle {\text{OTQ}} \to ({\text{a)}}$
Similarly,
In $\vartriangle {\text{PRT and }}\vartriangle {\text{QRT}}$
RT = RT (Common side)
$\angle {\text{OTP = }}\angle {\text{OTQ}}$ (from a)
TP = TQ (Tangents drawn from an external point to a circle are equal in length)
$\therefore \vartriangle {\text{PRT }} \cong {\text{ }}\vartriangle {\text{QRT}}$(by SAS congruency)
[SAS postulate states that if two corresponding sides and an included angle of two triangles are equal then they are congruent.]
By applying CPCT (Corresponding parts of congruent triangles)
${\text{PR = QR}} \to {\text{(b)}}$
Also, $\angle {\text{PRT = }}\angle {\text{QRT}}$ (by CPCT)
Now , we know
$\angle {\text{PRT + }}\angle {\text{QRT = 18}}{0^ \circ }{\text{ }}$ (Linear pair of angles)
$\Rightarrow 2\angle {\text{QRT = 18}}{0^ \circ } \\\ \Rightarrow \angle {\text{QRT = 9}}{0^ \circ } = \angle {\text{PRT}} \to (c) \\\$
From relation b and c , we can say that
OT is the right bisector of the line segment PQ.
Hence proved.

Note : Properties of congruent triangles along with all the postulates for congruence must be well known , also properties of the circle are must in order to solve such similar questions. Attention is to be given while selecting the triangles and their corresponding side and angles.