Question

From a point on the ground the angles of elevation of the bottom and top of a transmission tower fixed at the top of a 20m high building are ${45^ \circ }$ and ${60^ \circ }$, respectively. Find the height of the transmission tower.

Answer 1

We draw a diagram having transmission tower on the top of the building. We use the formula of tan of an angle in the right angle triangle and write the fraction for both the angles of elevations. Calculate the distance of the building from the point of observation from the first scenario having elevation angle ${45^ \circ }$ and use it in the second scenario having elevation angle ${60^ \circ }$.

• In a right angled triangle, tan of an angle is given by dividing perpendicular of triangle by base of triangle.

Complete step-by-step solution:
We draw a diagram for the given situation.
AB is the distance of the foot of the building from the point of observation. BC is the height of the building. CD is the transmission tower where C is the bottom of the tower and D is the top of the tower. We are given the length $BC = 20$m

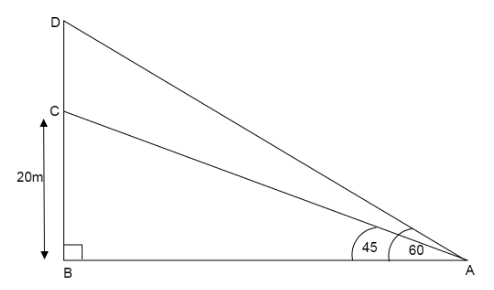
We know buildings make right angles with the ground, so we can say $\vartriangle ABC,\vartriangle ABD$are right angled triangles.
In right triangle $\vartriangle ABC$, $\angle BAC = {45^ \circ }$
We know tan of an angle is given by dividing perpendicular of triangle by base of triangle.
$\Rightarrow \tan {45^ \circ } = \dfrac{{BC}}{{AB}}$
We substitute the value of $\tan {45^ \circ } = 1$and $BC = 20$m in the equation
$\Rightarrow 1 = \dfrac{{20}}{{AB}}$
Cross multiply the values
$\Rightarrow AB = 20$m………………...… (1)
Now we know $BD = BC + CD$
$\Rightarrow BD = 20 + CD$...................… (2)
In right triangle$\vartriangle ABD$, $\angle BAD = {60^ \circ }$
We know tan of an angle is given by dividing perpendicular of triangle by base of triangle.
$\Rightarrow \tan {60^ \circ } = \dfrac{{BD}}{{AB}}$
We substitute the value of $\tan {60^ \circ } = \sqrt 3$and$AB = 20$ in the equation
$\Rightarrow \sqrt 3 = \dfrac{{BD}}{{20}}$
Substitute the value of BD from equation (2)
$\Rightarrow \sqrt 3 = \dfrac{{20 + CD}}{{20}}$
Cross multiply the values
$\Rightarrow 20\sqrt 3 = 20 + CD$
Shift all constants to one side of the equation
$\Rightarrow 20\sqrt 3 - 20 = CD$
Take 20 common in LHS
$\Rightarrow 20(\sqrt 3 - 1) = CD$
Put the value of $\sqrt 3 = 1.73$
$\Rightarrow 20(1.73 - 1) = CD$
$\Rightarrow 20 \times 0.73 = CD$
$\Rightarrow CD = 14.69$m

$\therefore$The height of the transmission tower CD is 14.69 m

Note: Many students don’t remember the values of trigonometric functions at common angles, they can take help of the table. Table for trigonometric functions like sine, cosine and tan at angles ${0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ }$ is

ANGLEFUNCTION	${0^ \circ }$	${30^ \circ }$	${45^ \circ }$	${60^ \circ }$	${90^ \circ }$
Sin	0	$\dfrac{1}{2}$	$\dfrac{1}{{\sqrt 2 }}$	$\dfrac{{\sqrt 3 }}{2}$	1
Cos	1	$\dfrac{{\sqrt 3 }}{2}$	$\dfrac{1}{{\sqrt 2 }}$	$\dfrac{1}{2}$	0
Tan	0	$\dfrac{1}{{\sqrt 3 }}$	1	$\sqrt 3$	Not defined