Question

From a point on the ground, the angles of elevation to the bottom and top of a tower fixed on the top of a 20m high building are $45{}^\circ$ and $60{}^\circ$ respectively. Find the height of the tower.

Answer 1

Hint: Assume that the height of the tower is h. Find $\tan \alpha$ in triangle ABD and $\tan \beta$ in triangle ACD. Use $\alpha =45{}^\circ$ and $\tan 45{}^\circ =1$ to find AD. Use $\beta =60{}^\circ$ and $\tan 60{}^\circ =\sqrt{3}$ to find the length of AC. Use BC = h = AC- AB to find the height of the tower. Verify your result.

Complete step-by-step answer:

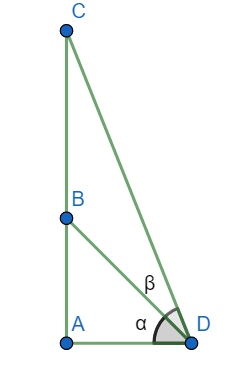
AB is a building of height 20m. On point B, a tower BC fixed. D is a point on the ground from which the angles of elevation to point B and C are $\alpha$ and $\beta$. Here $\alpha =30{}^\circ$ and $\beta =60{}^\circ$.
To determine: The height BC of the tower.
Let the height of the tower be h.
Now in triangle ABD, we have
$\tan \alpha =\dfrac{AB}{AD}$
Hence we have $AD=\dfrac{AB}{\tan \alpha }$
We know that $\tan 45{}^\circ =1$.
Hence $\tan \alpha =1$
Hence we have $AD=\dfrac{AB}{1}=AB$
Since AB is of length 20m, we have AD = 20m.
Now in triangle ACD, we have $\tan \beta =\dfrac{AC}{AD}$
Hence we have $AC=AD\tan \beta$
We know that $\tan \left( 60{}^\circ \right)=\sqrt{3}$
Hence $\tan \beta =\sqrt{3}$
Hence we have
$AC=AD\sqrt{3}$
Since AD = 20m, we have
$AC=20\sqrt{3}$
But AC = AB+BC = AB+h
Hence we have
$AB+h=20\sqrt{3}$
Since AB = 20m, we have
$20+h=20\sqrt{3}$
Subtracting 20 from both sides, we get
$h=20\sqrt{3}-20$
Taking 20 common from both the terms, we get
$h=20\left( \sqrt{3}-1 \right)m$
Hence the height of the tower $=20\left( \sqrt{3}-1 \right)m$
Note: [1] Verification:
Since AB = AD = 20m, ABD is a right-angled isosceles triangle and hence $\alpha =45{}^\circ$
Also in triangle ADC, we have
$\dfrac{AC}{AD}=\dfrac{20\sqrt{3}}{20}=\sqrt{3}$
Hence $\tan \beta =\sqrt{3}\Rightarrow \beta =60{}^\circ$
Hence our answer is verified to be correct.
[2] In questions of this type it is important to realise the diagram as shown above.