Question

From a point on the ground, the angle of elevation of the top of a tower is observed to be 60 degrees. From a point, 40m vertically above the first point of observation, the angle of elevation of the top of the tower is 30 degrees. Find the horizontal distance from the point of observation
A.$- 20\sqrt 3 m$
B.$\dfrac{{\sqrt 3 }}{{20}}m$
C.$- \dfrac{{\sqrt 3 }}{{20}}m$
D.$20\sqrt 3 m$

Answer 1

Hint : In this question we are supposed to find the horizontal distance from the point of observation which is AP. We will consider the triangle AQP and using angle QAP, we will find the values of required sides of the triangle.

Complete step-by-step answer :
Let point A is 40m above from point B.
Given: angle QAP = 60 degree
Angle QBR = 30 degree
AB = 40m So, PR will also be 40m

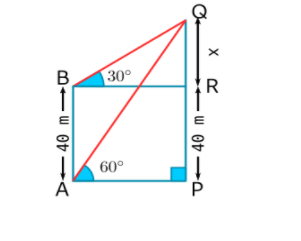
First, we will take the triangle QAP.
In $\vartriangle QAP$,
Take the angle QAP as tan60
$\tan 60^\circ = \dfrac{{PQ}}{{AP}}$
Value of tan 60 is $\sqrt 3$. So, replacing it in the above equation.
$\sqrt 3 = \dfrac{{PR + QR}}{{AP}}$
Value of PR is 40. So, replacing it in the above equation.
$\sqrt 3 = \dfrac{{40 + QR}}{{AP}}$
$\sqrt 3 AP = 40 + QR$------(1)
Now we will take triangle QBR.
In $\vartriangle QBR$
Take angle QBR as tan 30.
$\tan 30^\circ = \dfrac{{QR}}{{BR}}$
Value of tan30 is $\dfrac{1}{{\sqrt 3 }}$. And BR is equal to AP. So, replacing it in the above equation.
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{QR}}{{AP}}$
$AP = \sqrt 3 QR$-----(2)
Putting this value of AP in equation (1)
$\sqrt 3 \left( {\sqrt 3 QR} \right) = 40 + QR$
$3QR = 40 + QR$
$2QR = 40$
$QR = 20m$
Now, $AP = \sqrt 3 QR$
Value of QR is 20. So, putting it in the above equation.
$AP = \sqrt 3 \times 20$
$AP = 20\sqrt 3 m$
Value of horizontal distance from the point of observation is $20\sqrt 3 m$.
So, option (D) is the correct answer.
So, the correct answer is “Option D”.

Note : The angle of elevation is the angle formed by the horizontal line of sight and the horizontal plane for an object above the horizontal.
Values of trigonometric angles are used to solve these kinds of problems.