Question

From a point on the ground at a distance a from the foot of a pole, a ball is thrown at an angle of ${45^ \circ },$which just touches the top of the pole and strikes the ground at a distance of b, on the other side of it. Find the height of the pole.

Answer 1

In the question, the thrown angle and also the ball touches the top of the pole and strikes the ground and the coordinates are given. By using the equation, we find the value of the height of the pole.

Formula used:
The expression for finding the equation of height is
$y = x\,\tan \alpha \left( {1 - \dfrac{x}{R}} \right)$
Where,
$R$ be the total length, $x$ be the length of the ball from starting and $\alpha$ be the thrown angle of the ball.

Complete step by step solution:

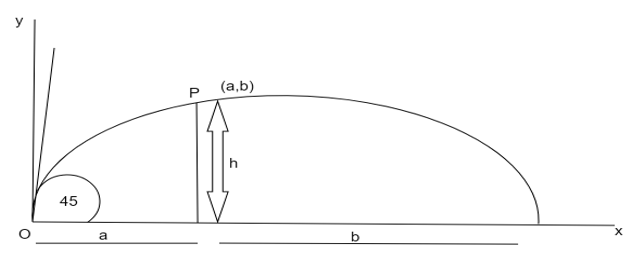
Given that the ball is thrown from the ground at a distance a foot of the pole and height of the pole is equal to the height of the axis.
Also, given that the angle of the ball thrown $\alpha = {45^ \circ }$
$y = x\,\tan \alpha \left( {1 - \dfrac{x}{R}} \right)..........\left( 1 \right)$
The coordinates of the point $P$are $\left( {a,b} \right)$
Since the top of the pole lies on the curve so we written the equation as,
Substitute all the values in the equation $\left( 1 \right)$
$h = a\,\tan {45^ \circ }\left( {1 - \dfrac{a}{{a + b}}} \right)$
Simplify the equation by using the trigonometric formula we get,
$h = a\,\left( {1 - \dfrac{a}{{a + b}}} \right)$
Simplify the above equation by taking the L.C.M we get,
$h = a\,\left( {\dfrac{{a + b - a}}{{a + b}}} \right)$
Simplify the equation we get,
$h = \,\left( {\dfrac{{ab}}{{a + b}}} \right)$

Therefore, the height of the pole is $\,\left( {\dfrac{{ab}}{{a + b}}} \right)$.

Note: In the question, the ball strikes at the top so we take the top of the pole as the height. After it touches the pole it strikes the ground so we add the distance from the starting by using the throne angle of the ball and the height of the pole has been calculated.