Question

From a fixed support, two small identical spheres are suspended by means of strings of length 1m each. They are pulled aside as shown and then released. B is the mean position. Then the two spheres collide.

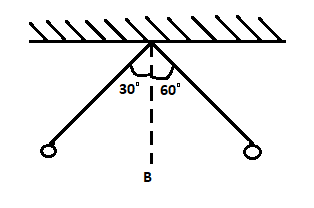
A. at B after 0.25 second
B. at B after 0.5 second
C. On the right side of B after some time.
D. On the right side of B when the strings are inclined at 15° with B.

Answer 1

The time period of oscillation of the simple pendulum depends on the length of the pendulum and as length for both the spheres are same that is why period of oscillation will be same for both the spheres.

Complete step by step solution:
The time taken by the simple pendulum from the point of release to the mean position is one fourth of the time period of the oscillation of the pendulum. So, both the spheres will reach point B at the same time regardless of the angle from the vertical where it is released.
Given that the length of the string is 1 m.
Using the formula for time period of simple pendulum,
$T=2\pi \sqrt{\dfrac{l}{g}}$
Where,
$l$ is the length of the pendulum.
$g$ is the acceleration due to gravity = 9.8m/s2
$T$ is the time period of oscillation.
Putting the value of $l\text{ and }g$we get,
$\begin{aligned} & T=2\pi \sqrt{\dfrac{1}{9.8}}s \\\ & =2s \end{aligned}$
As time taken from the extreme position to the mean position is one fourth of the time period of the oscillation.
Therefore time taken for the sphere to reach the point B is t.
$t=\dfrac{T}{4}$
Putting the value of the time period $T=2\operatorname{s}$ we get the value of the time taken by spheres to reach the point B as,
$\begin{aligned} & t=\dfrac{2s}{4} \\\ & =0.5s \end{aligned}$

Hence, the spheres will collide at point B after 0.5s.

Note: - Time period of the oscillation is dependent on length of the string.
- Time period of the oscillation is independent of the amplitude.
- Time taken to move from extreme position to the mean position is one fourth of the total time period of the oscillation.