Question

From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the center is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the center?

Answer 1

We need to understand the relation between the amount of substance that makes up an object – the mass – and the moment of inertia of the same object. From this we can find the moment of inertia of the disc when a portion of mass is removed.

Complete answer:
We are given a disc which has a radius of R units and mass M. It is said that a circular portion is carved out from the disc such that the rim of the sphere passes through the center of the circle with a diameter R itself.
We know that the moment of inertia of a solid disc is given as the half of the product of the mass and the square of the radius of the disc.
i.e.,
${{I}_{disc}}=\dfrac{M{{R}^{2}}}{2}$

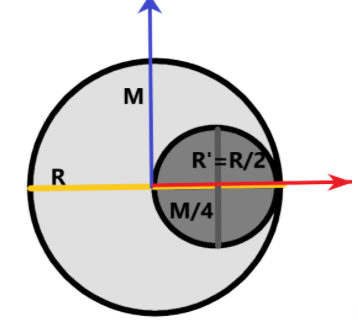
The mass removed when carving out the spherical portion is given as –

& Mass\propto Radiu{{s}^{2}} \\\ & \Rightarrow {{M}_{left}}\propto {{(\dfrac{R}{2})}^{2}} \\\ & \Rightarrow {{M}_{removed}}\propto \dfrac{{{R}^{2}}}{4} \\\ & \therefore {{M}_{removed}}=M\times \dfrac{1}{4} \\\ \end{aligned}$$ Now, we can find the moment of inertia of the spherical portion that is removed using the perpendicular axes theorem as – $$\begin{aligned} & {{I}_{removed}}=\dfrac{{{M}_{removed}}R{{'}^{2}}}{2}+{{M}_{removed}}R{{'}^{2}} \\\ & \Rightarrow {{I}_{removed}}=\dfrac{M}{4}\dfrac{{{(\dfrac{R}{2})}^{2}}}{2}+\dfrac{M}{4}{{(\dfrac{R}{2})}^{2}} \\\ & \therefore {{I}_{removed}}=\dfrac{3M{{R}^{2}}}{32} \\\ \end{aligned}$$ Now, we can find the moment of inertia of the remaining disc by subtracting the initial moment of inertia from the moment of inertia of the removed portion as – $$\begin{aligned} & I={{I}_{disc}}-{{I}_{removed}} \\\ & \Rightarrow I=\dfrac{M{{R}^{2}}}{2}-\dfrac{3M{{R}^{2}}}{32} \\\ & \therefore I=\dfrac{13M{{R}^{2}}}{32} \\\ \end{aligned}$$ So, the moment of inertia of the remaining portion of the disc is $$\dfrac{13}{16}$$ times the initial moment of inertia of the disc. This is the required solution. **Note:** The perpendicular axes theorem says that the moment of inertia of a body along a third axis which is perpendicular to two other axes of known moment of inertia and mutually perpendicular will be the sum of the moment of inertia along these axes.