Question

From a circular disc of radius R and mass 9M, a small disc of radius $\dfrac{R}{3}$ is removed from the disc, the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is:

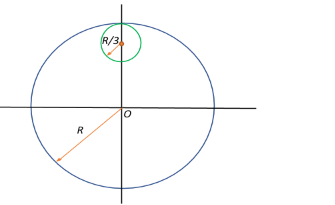
A. $4MR^2$
B. $\dfrac{40}{9}MR^2$
C. $10MR^2$
D. $\dfrac{37}{9}MR^2$

Answer 1

First determine the moment of inertia MI of the entire disc about the given axis of rotation. Then, determine the mass of the disc that was cut out by taking the fractional area of the cut-out disc and multiplying it by the entire mass of the big disc. Following this, use the parallel axis theorem to determine the MI of the disc about the given axis of rotation. To this end, subtract the MI of the cut-out disc from the MI of the whole disc to obtain the appropriate MI of the remaining disc about the given axis of rotation.
Formula used:
Moment of inertia of circular disc $I = \dfrac{1}{2}mr^2$
Parallel axis theorem: $I = I_c +Mh^2$

Complete answer:
We know that the moment of inertia MI of a circular disc about an axis perpendicular to the disc and passing through the centre O is given as:
$I = \dfrac{1}{2}mr^2$
Given that mass of the disc m = 9M and radius R:
$I_1= \dfrac{1}{2} \times 9M \times R^2 = \dfrac{9}{2}MR^2$
Let us now find the MI of the disc that was cut out. The radius of the cut out disc is given as $\dfrac{R}{3}$
The mass of the disc that was cut out can be given as:
$m_{cut} = \dfrac{area\;of\;cutout\;disc}{Total\;area\;of\;disc} \times total\;mass\;of\;disc = \dfrac{\pi\left(\dfrac{R}{3}\right)^2}{\pi R^2} \times 9M$
$\Rightarrow m_{cut} = \dfrac{\pi R^2}{9\pi R^2} \times 9M \Rightarrow m_{cut} = M$
Now, the parallel axis theorem states that the moment of inertia of a body about an axis parallel to an axis passing through the centre of mass will be equal to the sum of the moment of inertia of the body about an axis passing through the centre of mass, and the product of the mass and the square of the distance between the two axis. It is given as:
$I = I_c +mh^2$, where $I_c$ is the moment of inertia of the body about its centre, m is the mass of the body and h is the distance between the two axes.

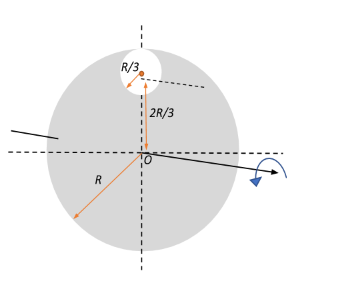
Note that the centre of the cut-out disc through which its centre of mass axis passes through is at a distance $R - \dfrac{R}{3} = \dfrac{2R}{3}$ from the centre of the big disc.
$I_2 = \dfrac{1}{2}\times M \times \left(\dfrac{R}{3}\right)^2 + M \times \left(\dfrac{2R}{3}\right)^2$
$\Rightarrow I_2 = \dfrac{MR^2}{9} \left(\dfrac{1}{2}+4\right) = \dfrac{MR^2}{9}. \dfrac{9}{2} = \dfrac{1}{2}MR^2$
Therefore, the net moment of inertia of the remaining disc will be:
$I = I_1 -I_2 = \dfrac{9}{2}MR^2 - \dfrac{1}{2}MR^2 = \dfrac{9MR^2-MR^2}{2} = \dfrac{8MR^2}{2}$
$\Rightarrow I = 4MR^2$

So, the correct answer is “Option A”.

Note:
Do not get confused between the parallel axis and the perpendicular axis theorems. We use the parallel axis theorem when we want to find the moment of inertia of a body about the axis that is parallel to the axis of the known moment of inertia of the body and passes through the centre of mass of the object. We use the perpendicular axis theorem when we want to find the moment of inertia of a body about the axis that is perpendicular to the axis of the known moment of inertia of the body and passes through the centre of mass of the object.
Moment of inertia of a body using Parallel axis theorem: $I = I_c +Mh^2$, where $I_c$ is the moment of inertia of the body about its centre, M is the mass of the body and h is the distance between the two axes.
Moment of inertia of a body using Perpendicular axis theorem: $I = I_1 +I_2$, where $I_1$ and $I_2$ are the moment of inertia of the body in the plane to which the $I$ that we have to find is perpendicular.