Question

From a circular disc of radius R and mass 9M, a small disc of mass M and radius $\dfrac{R}{3}$ is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of disc and passing through its centre is
(a) $\dfrac{40}{9}M{{R}^{2}}$
(b) $M{{R}^{2}}$
(c) $4M{{R}^{2}}$
(d) $\dfrac{4}{9}M{{R}^{2}}$

Answer 1

Hint: First of all, we will find the moment of inertia of a disc having $9M$mass and radius R, then we will find the moment of inertia of the small disc which is removed. Then we will take the difference of moment of inertia, so, finally we will get the Moment of inertia of the remaining disc.

Formula used: $I=\dfrac{1}{2}M{{R}^{2}}$

Complete step by step answer:
In question we are given that From a circular disc of radius R and mass $9M$, a small disc of mass M and radius $\dfrac{R}{3}$ is removed concentrically and we are asked to find the moment of inertia of remaining disc along the axis perpendicular to its plane. So, first of all we will draw a figure for our simplicity

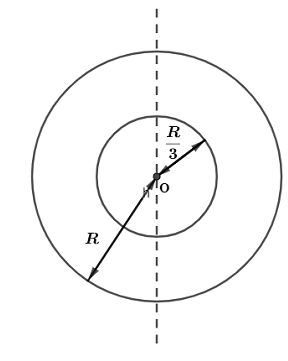
Now, let’s consider the mass of the original disc as ${{M}_{1}}$ and ${{M}_{2}}$ is the mass of the disc which is removed. Now, moment of inertia of disc rotating along the axis passing through its centre and perpendicular to the plane, can be given by the formula,
$I=\dfrac{1}{2}M{{R}^{2}}$
Now, moment of inertia of original disc can be given as,
${{I}_{1}}=\dfrac{1}{2}{{M}_{1}}{{R}^{2}}$
Where, ${{M}_{1}}=9M$ and radius is R, on substituting these values we will get,
${{I}_{1}}=\dfrac{9}{2}M{{R}^{2}}$
Now, the moment of inertia of remaining disc can be given as,
${{I}_{2}}=\dfrac{1}{2}{{M}_{2}}{{R}^{2}}$
where, ${{M}_{2}}=M$ and radius is $\dfrac{R}{3}$, on substituting these values we will get,
${{I}_{2}}=\dfrac{1}{2}M{{\left( \dfrac{R}{3} \right)}^{2}}$
${{I}_{2}}=\dfrac{1}{18}M{{R}^{2}}$
Now, taking difference of moment of inertia of original and removed part we fill find the moment of inertia of remaining disc, which can be given as,
$I={{I}_{1}}-{{I}_{2}}$
On substituting the values, we will get,
$I=\dfrac{9}{2}M{{R}^{2}}-\dfrac{1}{18}M{{R}^{2}}$
$I=\dfrac{81-1}{18}M{{R}^{2}}\Rightarrow I=\dfrac{80}{18}M{{R}^{2}}$
$\Rightarrow I=\dfrac{40}{9}M{{R}^{2}}$.
Thus, moment of inertia of remaining disc is $\dfrac{40}{9}M{{R}^{2}}$
Hence, option (a) is the correct answer.

Note: Students might try to solve the sum in shorter way by directly deducting the masses and radius of the disc such as, $I=\dfrac{1}{2}\left( 9-1 \right)M{{\left( R-\dfrac{R}{3} \right)}^{2}}\Rightarrow I=\dfrac{8}{2}M\left( \dfrac{2R}{3} \right)=\dfrac{16}{9}M{{R}^{2}}$ but this will give wrong answer because the area of the disc also comes into consideration while solving in this way so, to avoid the errors students must solve using the above derived method.