Question

From a circular disc of radius $R$ and mass $9M$, a small disc of radius $\dfrac{R}{3}$​ is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc passing through the centre of the disc is:

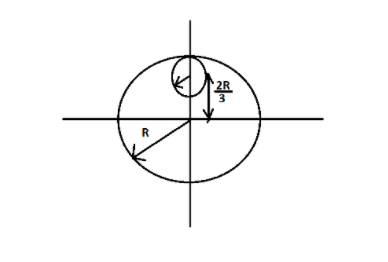
A) $10M{R^2}$
B) $\dfrac{{37}}{9}M{R^2}$
C) $4M{R^2}$
D) $\dfrac{{40}}{9}M{R^2}$

Answer 1

To solve this question, we have to first find the moment of inertia of the larger disc by using the direct formula of moment of inertia for a disc. After that we can find the mass of the smaller disc with radius $\dfrac{R}{3}$ which is removed from the larger disc. Then by using Parallel axis Theorem, we can find the moment of inertia of the remaining part of the disc.

Formula Used:
Moment of inertia of a disc about perpendicular axis,
$I = \dfrac{1}{2}M{R^2}$
Where $I$ is the moment of inertia of a disc about a perpendicular axis, $M$ is the mass of the disc and $R$ is the radius of the disc.
Parallel Axis Theorem,
$I = {I_c} + M{H^2}$
Here $I$ is the moment of inertia of the body, ${I_c}$ is the moment of inertia of the body around the centre, $M$ is the mass of the body and $H$ is the distance of the body from the centre.

Complete step by step answer:
We know that the moment of inertia of complete disc about a perpendicular axis passing through centre is given as
$I = \dfrac{1}{2}M{R^2}$
Where $I$is the moment of inertia of a disc about a perpendicular axis, $M$ is the mass of the disc and $R$ is the radius of the disc.
So the moment of inertia of the complete disc ${I_c}$ with $M = 9M$ and $R = R$is,
$\Rightarrow {I_c} = \dfrac{1}{2} \times M \times {R^2} = \dfrac{1}{2} \times 9M \times {R^2} = \dfrac{{9M{R^2}}}{2}$
Now we can find the mass of the cut out disc which will be a fraction of the whole mass. So, mass of cut out disc ${M_o}$ with radius $\dfrac{R}{3}$ is
$\Rightarrow {M_0} = \dfrac{{9M}}{{\pi {R^2}}} \times \pi \dfrac{{{R^2}}}{9} = M$
So the mass of the removed piece of the disc will be $M$
Using parallel axis theorem we can calculate the moment of inertia of the smaller cut out circle. Substituting the values of mass of the removed disc as $M$ and the distance from the centre axis as $\dfrac{{2R}}{3}$ ($H = R - \dfrac{R}{3}$ ), we get the value of inertia of the removed disc to be,
$\Rightarrow {I_o} = {I_c} + M{H^2} = \dfrac{1}{2}M{R^2} + M{(\dfrac{{2R}}{3})^2} = \dfrac{1}{2}M{R^2}$
Therefore the moment of inertia of the remaining disc is,
${I_r} = {I_c} - {I_o} = 4M{R^2}$

Hence, option (C) is the correct option..

Note: While calculating the moment of inertia for any disc at a distance from the centre, always use the parallel axis theorem. Always be careful while taking the distance from the centre of the axis to the centre of the disc as the wrong value of the distance will give incorrect answers. Also take care of the mass while calculating the value of a body using parallel axis theorem.