Question
Question: $\frac{(x^2-4)^{30}(x^2-9)^9(x^2-3x+2)^{17}(3x^2+10)^{10}}{(x^2-5x+6)^{52}(x^2-25)^{60}(x^2+10)^{11}...
(x2−5x+6)52(x2−25)60(x2+10)11(x2−4)30(x2−9)9(x2−3x+2)17(3x2+10)10≤0
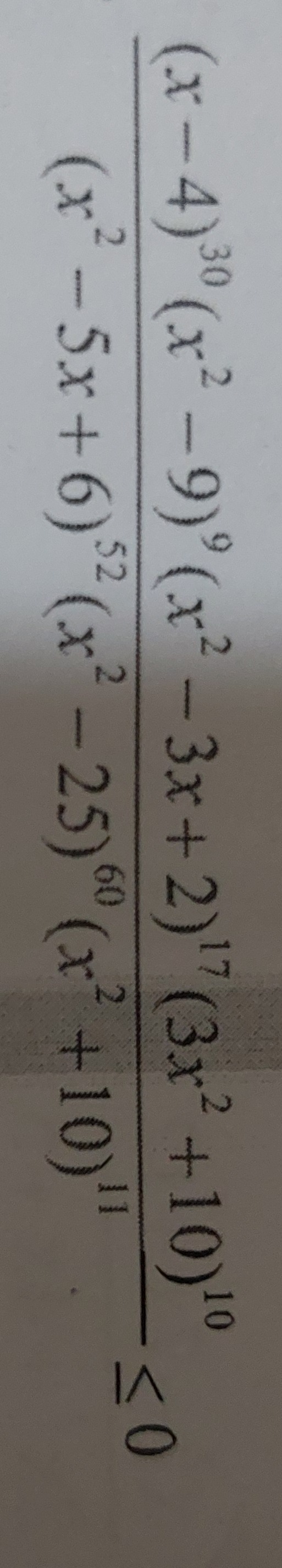
[-3, 1] ∪ (2, 3)
Solution
The given inequality is (x2−5x+6)52(x2−25)60(x2+10)11(x2−4)30(x2−9)9(x2−3x+2)17(3x2+10)10≤0.
Factorize the expressions: x2−4=(x−2)(x+2) x2−9=(x−3)(x+3) x2−3x+2=(x−1)(x−2) x2−5x+6=(x−2)(x−3) x2−25=(x−5)(x+5) 3x2+10>0 for all real x. x2+10>0 for all real x.
Substitute the factors into the inequality: ((x−2)(x−3))52((x−5)(x+5))60(x2+10)11((x−2)(x+2))30((x−3)(x+3))9((x−1)(x−2))17(3x2+10)10≤0
Combine terms with the same base: (x−2)52(x−3)52(x−5)60(x+5)60(x2+10)11(x−2)30(x+2)30(x−3)9(x+3)9(x−1)17(x−2)17(3x2+10)10≤0 (x−2)52(x−3)52(x−5)60(x+5)60(x2+10)11(x−2)47(x+2)30(x−3)9(x+3)9(x−1)17(3x2+10)10≤0
Since (3x2+10)10>0 and (x2+10)11>0 for all real x, we can divide by these terms: (x−2)52(x−3)52(x−5)60(x+5)60(x−2)47(x+2)30(x−3)9(x+3)9(x−1)17≤0
Simplify the terms with common bases in the numerator and denominator: (x−2)51(x−3)431(x+2)30(x+3)9(x−1)17(x−5)601(x+5)601≤0 (x−2)5(x−3)43(x−5)60(x+5)60(x+2)30(x+3)9(x−1)17≤0
Let f(x)=(x−2)5(x−3)43(x−5)60(x+5)60(x+2)30(x+3)9(x−1)17. The points where the denominator is zero must be excluded from the domain: x∈{2,3,5,−5}.
The terms with even powers are (x+2)30, (x−5)60, and (x+5)60. (x+2)30≥0. It is zero at x=−2. (x−5)60>0 for x=5. (x+5)60>0 for x=−5.
For x∈/{−5,−2,5}, the sign of f(x) is the same as the sign of (x−2)5(x−3)43(x+3)9(x−1)17. Let g(x)=(x−2)5(x−3)43(x+3)9(x−1)17. The critical points for g(x) are the roots of the numerator and denominator: x=−3,1,2,3. These points divide the number line into intervals: (−∞,−3),(−3,1),(1,2),(2,3),(3,∞). The powers of the factors in g(x) are all odd, so the sign of g(x) changes at each critical point. Let's test a value in (3,∞), e.g., x=4: g(4)=(4−2)5(4−3)43(4+3)9(4−1)17=(+)5(+)43(+)9(+)17=++=+. The sign of g(x) in the intervals is: (−∞,−3): + (−3,1): − (1,2): + (2,3): − (3,∞): +
We want f(x)≤0. This occurs when g(x)<0 or when f(x)=0.
Case 1: g(x)<0. This happens for x∈(−3,1)∪(2,3). We must exclude the points where the original denominator is zero: x∈{2,3,5,−5}. The intervals (−3,1) and (2,3) do not contain 5 or −5. The points 2 and 3 are the endpoints of the intervals, and they are excluded from the intervals. So, x∈(−3,1)∪(2,3) is part of the solution.
Case 2: f(x)=0. f(x)=0 when the numerator is zero and the denominator is non-zero. Numerator of f(x) is (x+2)30(x+3)9(x−1)17. It is zero at x=−2,x=−3,x=1. Denominator of f(x) is (x−2)5(x−3)43(x−5)60(x+5)60. It is zero at x=2,3,5,−5. The values where the numerator is zero but the denominator is non-zero are {−2,−3,1}. These points are solutions.
Combining the results from Case 1 and Case 2: The solution set is ((−3,1)∪(2,3))∪{−2,−3,1}. Let's combine the intervals and points: (−3,1)∪{−3,1}=[−3,1]. So the solution is [−3,1]∪(2,3)∪{−2}. Since −2 is in the interval [−3,1], the union is simply [−3,1]∪(2,3).
We should double-check the excluded points from the original inequality denominator: x∈{2,3,5,−5}. Our solution set [−3,1]∪(2,3) does not include 2,3,5,−5. The point x=−2 is included in [−3,1]. Let's check the original inequality at x=−2. Numerator at x=−2: ((−2)2−4)30(…)=(4−4)30(…)=0. Denominator at x=−2: ((−2)2−5(−2)+6)52((−2)2−25)60((−2)2+10)11=(4+10+6)52(4−25)60(4+10)11=(20)52(−21)60(14)11=0. So, at x=−2, the inequality is non-zero0≤0, which is 0≤0, which is true. So, x=−2 is indeed a solution. It is included in the interval [−3,1].
The final solution set is [−3,1]∪(2,3).
