Question
Question: $\frac{x+1}{(x-1)^2}<1$...
(x−1)2x+1<1
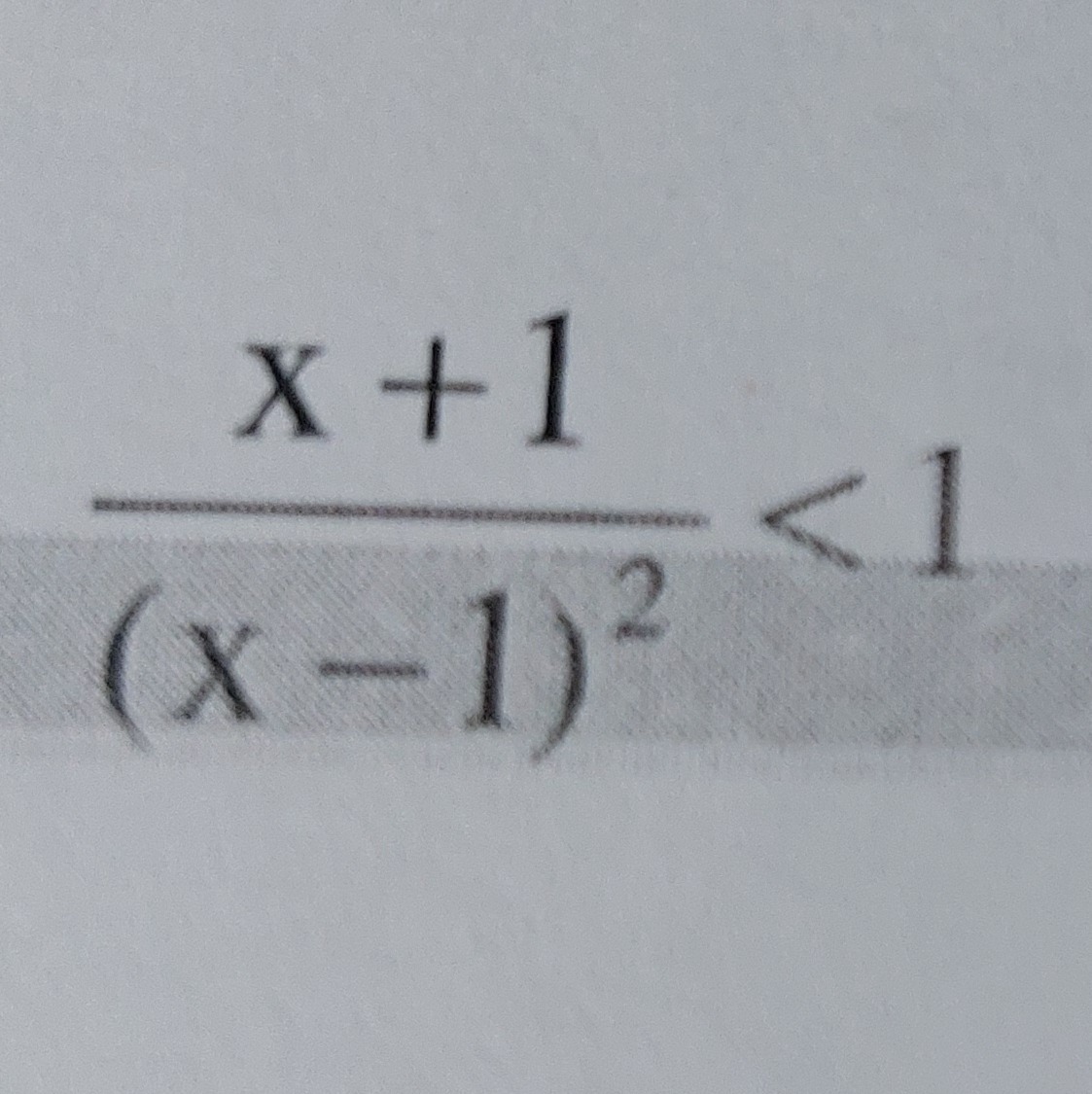
(−∞,0)∪(3,∞)
Solution
To solve the inequality (x−1)2x+1<1, we follow these steps:
-
Rewrite the inequality so that one side is zero: (x−1)2x+1−1<0.
-
Combine the terms on the left side into a single fraction: (x−1)2x+1−(x−1)2<0 (x−1)2x+1−(x2−2x+1)<0 (x−1)2x+1−x2+2x−1<0 (x−1)2−x2+3x<0 (x−1)2x(3−x)<0.
-
Find the critical points by setting the numerator and denominator to zero:
- Numerator: x(3−x)=0⟹x=0 or x=3.
- Denominator: (x−1)2=0⟹x=1.
-
Use the critical points to divide the number line into intervals: (−∞,0), (0,1), (1,3), (3,∞).
-
Test the sign of the expression (x−1)2x(3−x) in each interval. Note that (x−1)2>0 for x=1, so the sign is determined by x(3−x). We need x(3−x)<0.
-
Analyze the sign of x(3−x). This is a downward-opening parabola with roots at x=0 and x=3. Thus, x(3−x)<0 when x<0 or x>3.
-
The solution intervals are (−∞,0) and (3,∞). The point x=1 must be excluded, but it is not in these intervals.
-
Therefore, the solution set is the union of these intervals: (−∞,0)∪(3,∞).
Final Answer: (−∞,0)∪(3,∞)
