Question
Question: $\frac{(x-4)^{30}(x^2-9)(x^2-3x+2)^{17}}{(x^2-5x+6)^{52}(x^2-25)^{60}(x^2+10)^{11}} \le 0$...
(x2−5x+6)52(x2−25)60(x2+10)11(x−4)30(x2−9)(x2−3x+2)17≤0
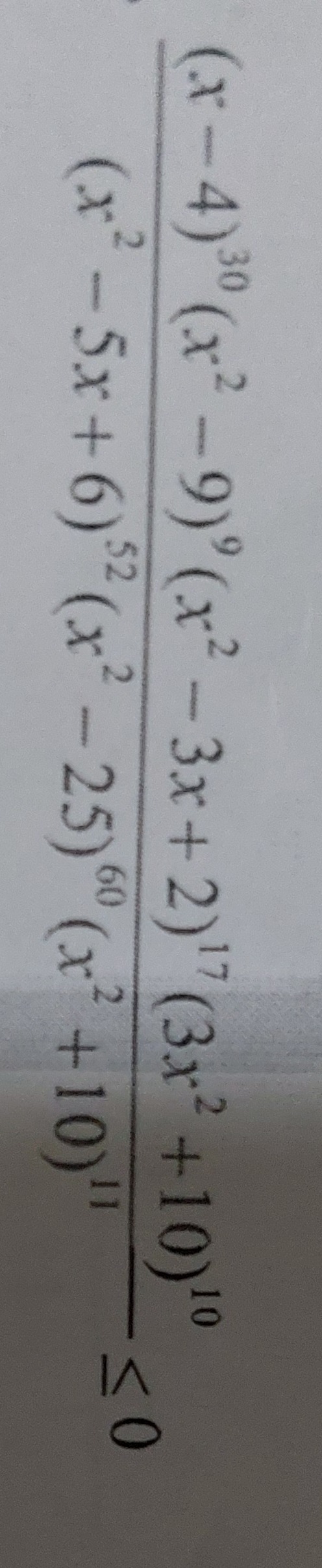
[-3, 1] ∪ (2, 3) ∪ {4}
Solution
The given inequality is (x2−5x+6)52(x2−25)60(x2+10)11(x−4)30(x2−9)(x2−3x+2)17≤0.
Factorize the polynomials:
x2−9=(x−3)(x+3)
x2−3x+2=(x−1)(x−2)
x2−5x+6=(x−2)(x−3)
x2−25=(x−5)(x+5)
x2+10 is always positive for real x.
Substitute the factors into the inequality:
((x−2)(x−3))52((x−5)(x+5))60(x2+10)11(x−4)30((x−3)(x+3))((x−1)(x−2))17≤0
Combine terms with the same base:
(x−2)52(x−3)52(x−5)60(x+5)60(x2+10)11(x−4)30(x−3)1(x+3)1(x−1)17(x−2)17≤0
Since (x2+10)11>0, we can ignore it for the sign analysis.
(x−2)52(x−3)52(x−5)60(x+5)60(x−4)30(x−3)(x+3)(x−1)17(x−2)17≤0
Simplify by canceling terms with common bases (subtracting exponents):
(x−2)52−17(x−3)52−1(x−5)60(x+5)60(x−4)30(x+3)(x−1)17≤0
(x−2)35(x−3)51(x−5)60(x+5)60(x−4)30(x+3)1(x−1)17≤0
Let f(x)=(x−2)35(x−3)51(x−5)60(x+5)60(x−4)30(x+3)1(x−1)17.
The critical points are the values of x where the numerator or denominator is zero: −5,−3,1,2,3,4,5.
The points where the denominator is zero must be excluded from the solution: x=2,3,5,−5.
We analyze the sign of f(x) using the wavy curve method based on the critical points and the powers of the factors:
Critical points in increasing order: −5,−3,1,2,3,4,5.
Powers of the corresponding factors:
(x+5)60 (even power)
(x+3)1 (odd power)
(x−1)17 (odd power)
(x−2)35 (odd power)
(x−3)51 (odd power)
(x−4)30 (even power)
(x−5)60 (even power)
Let's determine the sign of f(x) in the interval (5,∞). For x>5, all factors are positive, so f(x)>0.
Now, we move from right to left across the critical points, changing the sign if the power of the corresponding factor is odd, and keeping the sign if the power is even.
-
At x=5 (power 60, even): sign does not change. Interval (4,5): +.
-
At x=4 (power 30, even): sign does not change. Interval (3,4): +.
-
At x=3 (power 51, odd): sign changes. Interval (2,3): −.
-
At x=2 (power 35, odd): sign changes. Interval (1,2): +.
-
At x=1 (power 17, odd): sign changes. Interval (−3,1): −.
-
At x=−3 (power 1, odd): sign changes. Interval (−5,−3): +.
-
At x=−5 (power 60, even): sign does not change. Interval (−∞,−5): +.
Summary of the sign of f(x):
f(x)>0 for x∈(−∞,−5)∪(−5,−3)∪(1,2)∪(3,4)∪(4,5)∪(5,∞).
f(x)<0 for x∈(−3,1)∪(2,3).
We want f(x)≤0. This includes intervals where f(x)<0 and points where f(x)=0.
From the sign analysis, f(x)<0 for x∈(−3,1)∪(2,3).
Now consider where f(x)=0. This happens when the numerator is zero and the denominator is non-zero.
Numerator is (x−4)30(x+3)(x−1)17. It is zero when x=4, x=−3, or x=1.
Denominator is (x−2)35(x−3)51(x−5)60(x+5)60. It is zero when x=2,3,5,−5.
The values where the numerator is zero are {−3,1,4}.
The values where the denominator is zero are {2,3,5,−5}.
The values where f(x)=0 are the values from {−3,1,4} that are not in {2,3,5,−5}. These are {−3,1,4}.
So, x=−3,1,4 are solutions.
Combining the intervals where f(x)<0 and the points where f(x)=0:
Solution set = (−3,1)∪(2,3)∪{−3,1,4}.
This can be written as [−3,1]∪(2,3)∪{4}.
The points where the original denominator is zero (x∈{2,3,5,−5}) are excluded from the solution, which is consistent with our solution set.
The final answer is [−3,1]∪(2,3)∪{4}.
