Question
Question: $\frac{(x-1)(x-2)(x-5)}{(2x+5)}>0$...
(2x+5)(x−1)(x−2)(x−5)>0
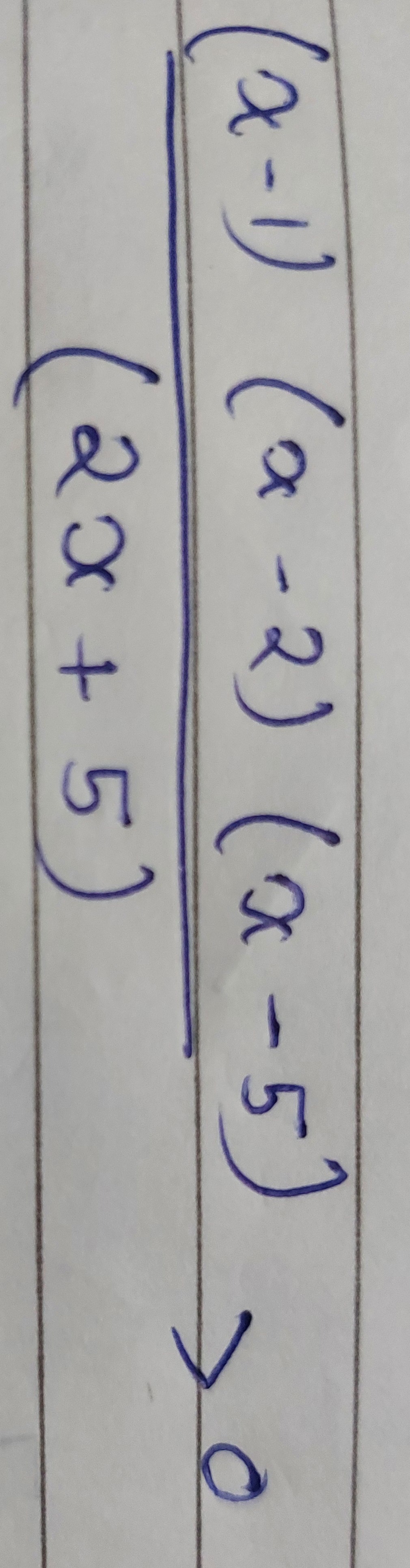
x∈(−∞,−5/2)∪(1,2)∪(5,∞)
Solution
We need to solve the inequality (2x+5)(x−1)(x−2)(x−5)>0.
Step 1: Find the critical points. These are the values of x where the numerator or the denominator is zero.
- Numerator is zero when (x−1)(x−2)(x−5)=0, which gives x=1, x=2, or x=5.
- Denominator is zero when 2x+5=0, which gives x=−25=−2.5.
Step 2: Arrange the critical points on the number line in increasing order. The critical points are −2.5,1,2,5. These points divide the number line into the following intervals:
(−∞,−2.5), (−2.5,1), (1,2), (2,5), (5,∞).
Step 3: Determine the sign of the expression (2x+5)(x−1)(x−2)(x−5) in each interval. We can use the wavy curve method or test a value within each interval.
Let f(x)=(2x+5)(x−1)(x−2)(x−5). All factors (x−1),(x−2),(x−5),(2x+5) have odd powers (power 1). The leading coefficients of all factors are positive.
For x>5 (the largest critical point), all factors are positive, so f(x)>0.
Since all critical points correspond to factors with odd powers, the sign of f(x) changes at each critical point as we move from right to left.
Sign analysis using the wavy curve method:
- In (5,∞), f(x)>0 (Positive).
- At x=5, the sign changes. In (2,5), f(x)<0 (Negative).
- At x=2, the sign changes. In (1,2), f(x)>0 (Positive).
- At x=1, the sign changes. In (−2.5,1), f(x)<0 (Negative).
- At x=−2.5, the sign changes. In (−∞,−2.5), f(x)>0 (Positive).
Step 4: Identify the intervals where the inequality (2x+5)(x−1)(x−2)(x−5)>0 is satisfied. This occurs when f(x)>0.
From the sign analysis, f(x)>0 in the intervals (−∞,−2.5), (1,2), and (5,∞).
The critical points themselves are not included in the solution because the inequality is strict (>0). The point x=−2.5 is excluded because the expression is undefined there.
The solution set is the union of these intervals.
The critical points of the rational inequality are the roots of the numerator (1,2,5) and the root of the denominator (−5/2). These points partition the number line into intervals. By analyzing the sign of the expression in each interval (e.g., using the wavy curve method, noting that all critical points come from factors with odd powers), we find the intervals where the expression is positive. The inequality (2x+5)(x−1)(x−2)(x−5)>0 is satisfied for x in (−∞,−5/2)∪(1,2)∪(5,∞).
