Question
Question: $\frac{sin3\theta-cos^3\theta}{sin\theta - cos\theta}-\frac{cos\theta}{\sqrt{1+cot^2\theta}}-2tan\th...
sinθ−cosθsin3θ−cos3θ−1+cot2θcosθ−2tanθcotθ=−1
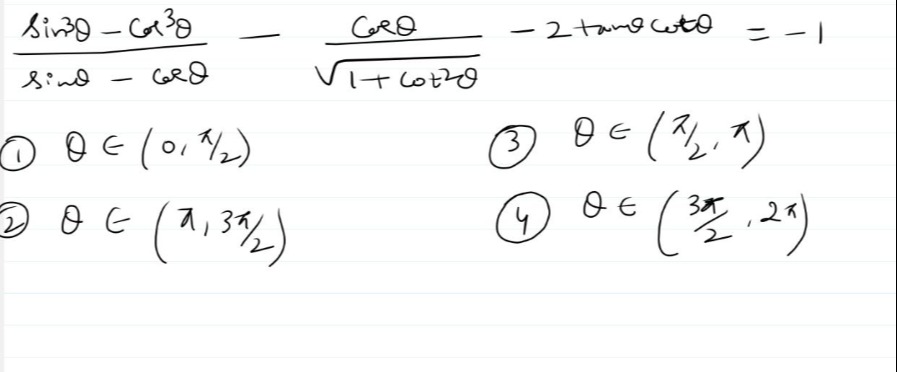
θ∈(0,2π)
θ∈(2π,π)
θ∈(π,23π)
θ∈(23π,2π)
①, ③
Solution
The given equation is: sinθ−cosθsin3θ−cos3θ−1+cot2θcosθ−2tanθcotθ=−1
Let's simplify each term:
Term 1: sinθ−cosθsin3θ−cos3θ Using the identity a3−b3=(a−b)(a2+ab+b2), we get: sinθ−cosθ(sinθ−cosθ)(sin2θ+sinθcosθ+cos2θ) Provided sinθ−cosθ=0 (i.e., θ=nπ+4π), this simplifies to: sin2θ+cos2θ+sinθcosθ=1+sinθcosθ
Term 2: 1+cot2θcosθ Using the identity 1+cot2θ=csc2θ: csc2θcosθ=∣cscθ∣cosθ Since cscθ=sinθ1, we have ∣cscθ∣=∣sinθ∣1. So, the term becomes cosθ∣sinθ∣.
Term 3: 2tanθcotθ Using the identity tanθcotθ=1: 2tanθcotθ=2(1)=2 This is valid provided tanθ and cotθ are defined, which means sinθ=0 and cosθ=0. So θ=n2π.
Now, substitute the simplified terms back into the equation: (1+sinθcosθ)−cosθ∣sinθ∣−2=−1 sinθcosθ−cosθ∣sinθ∣−1=−1 sinθcosθ−cosθ∣sinθ∣=0 Factor out cosθ: cosθ(sinθ−∣sinθ∣)=0 This equation holds if either cosθ=0 or sinθ−∣sinθ∣=0.
Case 1: cosθ=0 This implies θ=(2n+1)2π for integer n. For θ∈(0,2π), possible values are θ=2π and θ=23π. However, the original expression is undefined when cosθ=0 (because tanθ is undefined). Therefore, these values are not solutions.
Case 2: sinθ−∣sinθ∣=0 This implies sinθ=∣sinθ∣. This condition is true if and only if sinθ≥0. For θ∈(0,2π), sinθ≥0 when θ∈(0,π].
Now, we must consider the domain restrictions for the original expression:
- sinθ−cosθ=0⟹tanθ=1⟹θ=nπ+4π. For θ∈(0,2π), this means θ=4π and θ=45π.
- cotθ is defined ⟹sinθ=0⟹θ=nπ. For θ∈(0,2π), this means θ=π. (Note: θ=0,2π are already excluded by the open interval).
- tanθ is defined ⟹cosθ=0⟹θ=(2n+1)2π. For θ∈(0,2π), this means θ=2π and θ=23π.
Combining the condition sinθ≥0 (i.e., θ∈(0,π]) with the domain restrictions: We must exclude 4π, 2π, and π from the interval (0,π]. So, the solution set for θ is θ∈(0,4π)∪(4π,2π)∪(2π,π).
Let's check the given options: ① θ∈(0,2π): This interval is (0,2π). The solution set within this interval is (0,4π)∪(4π,2π). This option contains the values that are solutions, but also includes the excluded point 4π. However, if the question asks for an interval where the equation holds except for specific points, this is a common way to represent it.
③ θ∈(2π,π): This interval is (2π,π). All values in this interval satisfy sinθ>0. The excluded points 4π,45π,2π,π,23π are not in this open interval. So, for all θ∈(2π,π), the equation holds.
② θ∈(π,23π): In this interval, sinθ<0. So sinθ−∣sinθ∣=sinθ−(−sinθ)=2sinθ. The equation becomes cosθ(2sinθ)=0. This implies either cosθ=0 or sinθ=0. For θ∈(π,23π), cosθ<0 and sinθ<0, so neither is zero. Thus, no solutions in this interval.
④ θ∈(23π,2π): In this interval, sinθ<0. Similar to option ②, the equation becomes 2sinθcosθ=0, which has no solutions in this interval.
Therefore, the intervals where the equation holds are (0,4π)∪(4π,2π)∪(2π,π). Both option ① and option ③ represent parts of this solution set. Option ① is (0,2π), which contains the solutions (0,4π)∪(4π,2π). Option ③ is (2π,π), which contains the solutions (2π,π).
Since the question asks to select the correct options, and both intervals are part of the solution set where the equation is true (excluding the points where the expression is undefined), both ① and ③ are correct.
