Question

$\frac{(n-1)(n-2)}{n^!+L-3n}$

$QS=(1.2)C_2+(1.3)C_3+...+(n-1) nC_n=?$

Answer 1

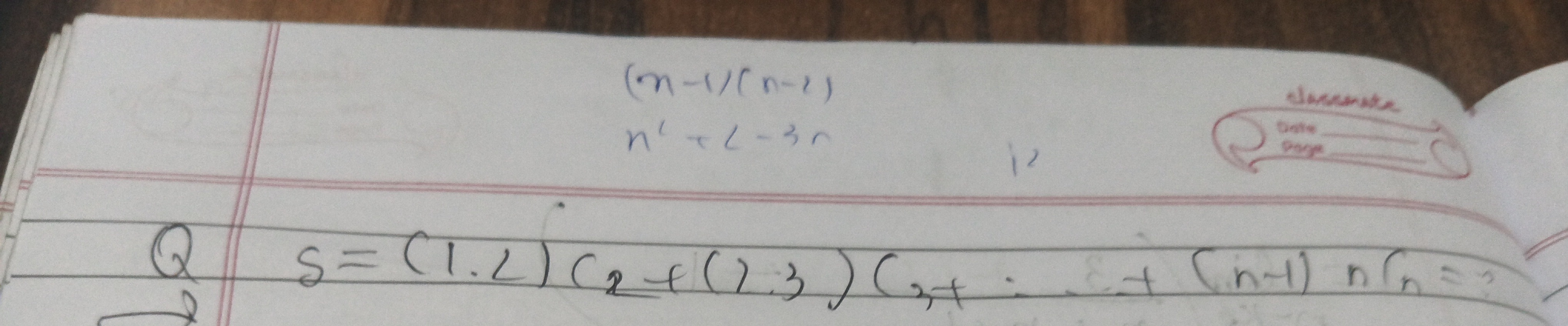
The sum $S = (1 \cdot 2)C_2 + (2 \cdot 3)C_3 + \dots + ((n-1) \cdot n)C_n$ is equal to $n(n-1)2^{n-2}$.

Answer 2

The problem asks us to find the sum of the series $S = (1 \cdot 2)C_2 + (2 \cdot 3)C_3 + \dots + ((n-1) \cdot n)C_n$, where $C_k$ denotes the binomial coefficient $\binom{n}{k}$. The general term of the series can be written as $T_k = (k-1)k C_k = (k-1)k \binom{n}{k}$. The sum starts from $k=2$ and goes up to $k=n$.

We use the identity for binomial coefficients: $k \binom{n}{k} = n \binom{n-1}{k-1}$. Let's apply this identity to the general term $T_k$: $T_k = (k-1) \left( k \binom{n}{k} \right)$ $T_k = (k-1) \left( n \binom{n-1}{k-1} \right)$ $T_k = n \left( (k-1) \binom{n-1}{k-1} \right)$

Now, we apply the identity again for the term $(k-1) \binom{n-1}{k-1}$. In this case, the 'n' in the identity becomes 'n-1' and the 'k' becomes 'k-1'. So, $(k-1) \binom{n-1}{k-1} = (n-1) \binom{(n-1)-1}{(k-1)-1} = (n-1) \binom{n-2}{k-2}$.

Substitute this back into the expression for $T_k$: $T_k = n (n-1) \binom{n-2}{k-2}$.

Now, we need to sum these terms from $k=2$ to $n$: $S = \sum_{k=2}^{n} T_k = \sum_{k=2}^{n} n(n-1) \binom{n-2}{k-2}$.

Since $n(n-1)$ is a constant with respect to $k$, we can take it out of the summation: $S = n(n-1) \sum_{k=2}^{n} \binom{n-2}{k-2}$.

Let $j = k-2$. When $k=2$, $j=0$. When $k=n$, $j=n-2$. So the summation becomes: $S = n(n-1) \sum_{j=0}^{n-2} \binom{n-2}{j}$.

We know the binomial theorem identity: $\sum_{r=0}^{m} \binom{m}{r} = 2^m$. In our sum, $m = n-2$. Therefore, $\sum_{j=0}^{n-2} \binom{n-2}{j} = 2^{n-2}$.

Substituting this back into the expression for $S$: $S = n(n-1) 2^{n-2}$.

The expression $\frac{(n-1)(n-2)}{n^!+L-3n}$ shown in the image is not related to the sum $S$ and is disregarded.

The final answer is $\boxed{n(n-1)2^{n-2}}$.

Explanation of the solution:

1. Identify the general term of the series as $T_k = (k-1)k \binom{n}{k}$.
2. Apply the identity $k \binom{n}{k} = n \binom{n-1}{k-1}$ twice to simplify $T_k$ to $n(n-1) \binom{n-2}{k-2}$.
3. Rewrite the sum $S$ using the simplified general term: $S = \sum_{k=2}^{n} n(n-1) \binom{n-2}{k-2}$.
4. Factor out the constant term $n(n-1)$ from the summation.
5. Change the index of summation from $k$ to $j=k-2$. This transforms the sum into $\sum_{j=0}^{n-2} \binom{n-2}{j}$.
6. Recognize this as the sum of all binomial coefficients for exponent $(n-2)$, which is equal to $2^{n-2}$ by the binomial theorem.
7. Combine the results to get the final sum $S = n(n-1)2^{n-2}$.